2-贝尔曼公式
笔记/强化学习

2-贝尔曼公式

为什么return是重要的 return是一个用来评估policy的好与坏的工具，只有通过比较return才能比较出policy的好与坏 return的计算

为什么return是重要的

return是一个用来评估policy的好与坏的工具，只有通过比较return才能比较出policy的好与坏

return的计算

image-20231219213608231

通过三种policy计算出三种不同的return从而评估三种policy谁好谁坏

方法一：by definition

image-20231219214011056

计算分别从s1,s2,s3,s4开始时的return，表示为v1,v2,v3,v4

方法二

image-20231219214355591

从不同状态出发得到return其实是依赖于从其他状态出发得到的return(Bootstrapping)

Bootstrapping

Bootstrapping:从自己出发,去不断的迭代所得到的结果

image-20231219215245043

这是一个对于一个非常具体定义情况下的贝尔曼公式

一个状态的value依赖于其他状态的value

image-20231219215511269

State value

单步过程

image-20231220130219282

St,At,Rt+1都是随机变量，这就代表了，我们可以对他们求期望一类的东西

每一步都跟随着probability distributions

  • St➡️At: Policy probability(策略可能性，也就是选取哪一种action的可能性)

  • St,At➡️Rt+1: Reward probability(reward可能性，也就是选取action后获得什么reward的可能性)

  • St,At➡️St+1:State transition probability(在状态St选择action At之后到达St+1的概率)

联合多步

image-20231220130836560

联合多步之后，就可以得到一个trajectory和一个discounted return

定义 State value

image-20231220131056556

👉State value实际上就是对于一个状态，我们可以得到很多个trajectory，那么我们也可以得到很多个return，对这些所有的return求一个期望(也就是平均值)，那么我们就可以得到这个状态的State value

example

image-20231220131347121

贝尔曼公式的推导

👉一句话描述：贝尔曼公式描述了不同的state value之间的关系

image-20231220131628251

当前的Gt就可以写成，Rt+1(当前立刻可以得到的reward)+γGt+1(从下一时刻出发所得到的return乘以一个discount rate)

根据公式来说我们就得到了两个期望

  • 一个是对于Rt+1(当前立刻可以得到的reward)

  • 一个是对于γGt+1(从下一时刻出发所得到的return乘以一个discount rate)

Rt+1(当前立刻可以得到的reward)

image-20231220132107936

  • 前面一项是在s take action a的概率和，也就是Policy probability

  • 而后一项是指在s take action a后获得reward r的概率 X reward r的值，也就是Reward probability * Reward value

γGt+1(从下一时刻出发所得到的return乘以一个discount rate)

image-20231220132700961

  • 前面一项指的是在s’处的state value

  • 后一项指的是在s处take action a的概率(Policy probability) * s在take action a之后到达s‘的概率(State transition probability),总的来说也就是在s到s’的总概率

👉这个总概率再乘以上s’处的state value，就得到了一个未来的reward

贝尔曼公式的表达式

image-20231220133533018

总的来说就是s处take action a的概率(Policy probability) * [当前reward + γ未来reward]，这个式子是对于状态空间中的所有state都成立的

计算例子1

image-20231220134009667

image-20231220134147288

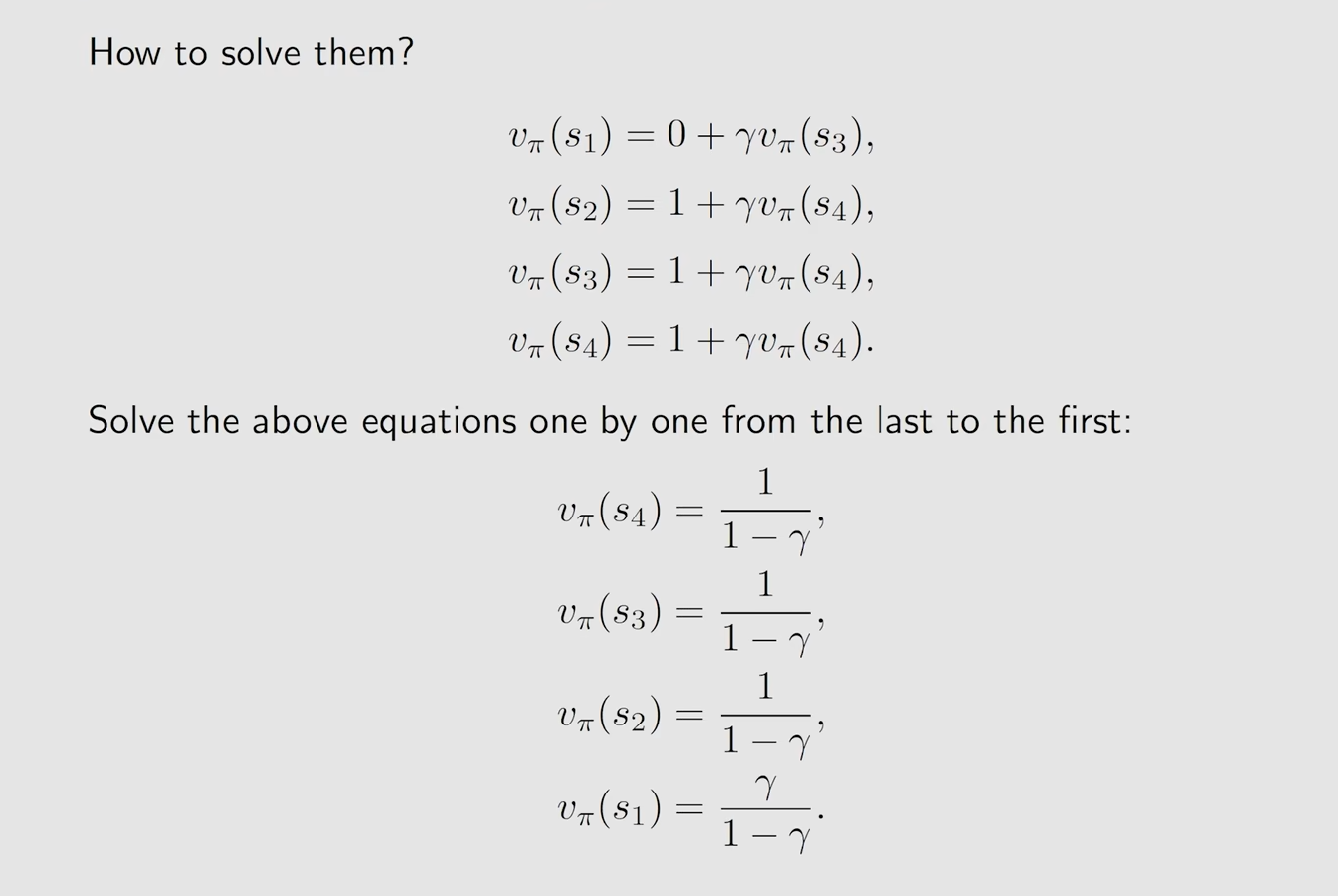
image-20231220134202790

image-20231220134247524

在我们计算了状态值之后要做什么?保持耐心(计算action value并改进Policy)

计算例子2

image-20231220134442789

image-20231220134524007

这个策略中所有的值加起来低于上一个策略，所以这个策略总的来说没有上一个策略好

贝尔曼公式的矩阵与向量形式

image-20231220134905395

image-20231220135142836

将一个状态空间中的所有state的贝尔曼公式全部写在一起，放在一个矩阵之中，就可以得到以上的一个形式

image-20231220135523568

求解state value

为什么要求解state value？

用于评估一个Policy的好与坏

方法一：求逆直接求解

image-20231220140021006

问题，求逆矩阵会很困难

方法二：迭代法求解

image-20231220140100487

通过先假设一个V0然后求出来一个V1，然后用假设出来的V1求出V2,以此类推不断迭代，最后就可以得到一个真实的Vk(State value)

例子

image-20231220140354681

在这里可以看到，越靠近目标点，state value就会逐渐变大

image-20231220140557790

所以，总的来说，state value的总和可以用来评价一个策略是好还是不好

Action value

  • State value：agent 从一个状态出发，所得到的一个 average return

  • Action value：agent 从一个状态出发，并且选择了一个action之后，所得到的 average return

总的来说，action value的用处就是用来评估这个action的好与坏，其实就是在选取了确切的action之后，计算当前的价值与未来的价值，越大则说明在当前和未来所得到的价值是更多的

定义

image-20231220141216235

从一个状态出发的state value = s处take action a的概率(Policy probability) * action value

image-20231220141443500

所以 action value = [当前reward + γ未来reward]

  • 如果我们知道了一个状态的所有action value可以求得所有的state value

  • 如果我们知道了一个状态的所有state value可以求得所有的action value

例子

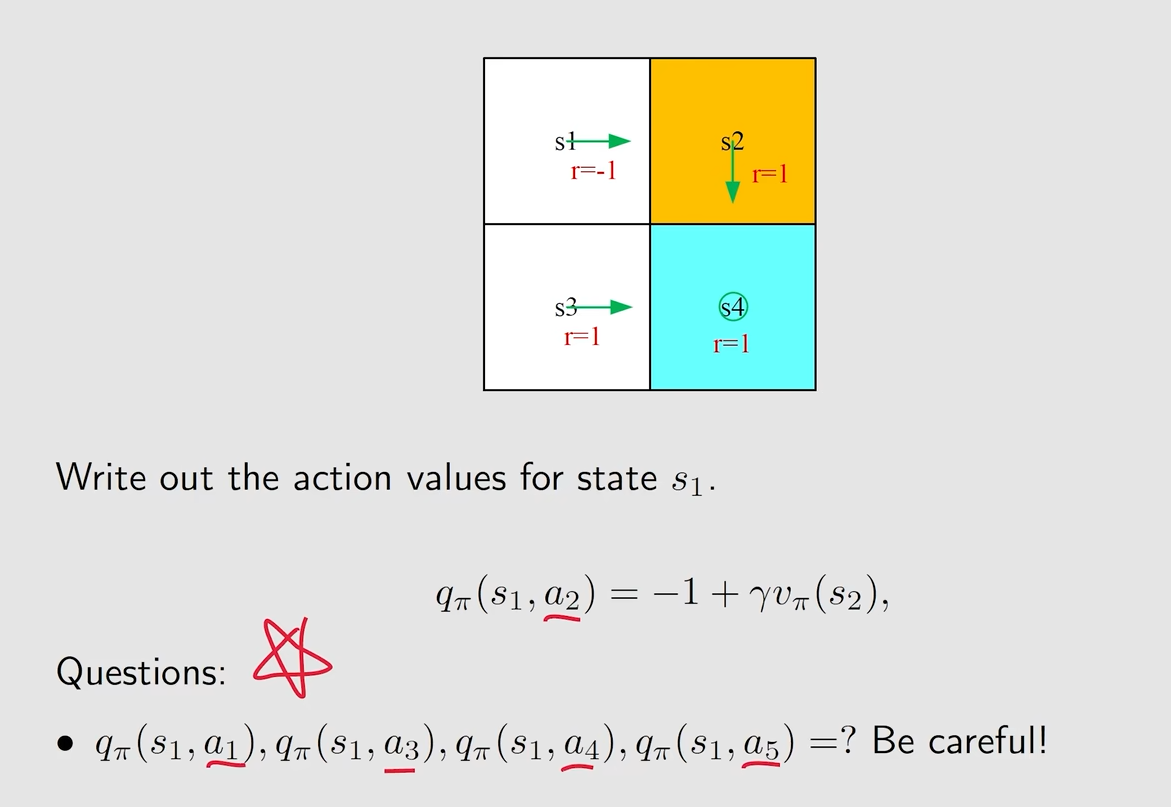
image-20231220141823177

总结


Comment