Value iteration(值迭代)

分为两个步骤：

1. 先通过给定Vk得到Πk+1

2. 然后再通过Πk+1求解出用于下次迭代的Vk+1

这里的Vk和Vk+1是一个估计的 state value，到迭代到最后收敛了，就是真实的 state value

Policy update

通过比较不同的action value，选取最大的那个action value的概率为1，则就可以取得这个部分的最大值

Value update

最后的这个Vk+1就是qk里面的最大值，因为除了最大值，其他的部分都是Policy概率都为0

过程总结

步骤：

1. 首先假定一个还没有收敛的Vk

2. 对于状态空间中的所有state的所有action，进行计算出action value

3. 然后选择最大的action value的那个action作为Policy(Policy update)

4. 然后使用所选择的Policy进行计算V-value(Value update)，实际上的V-value就是那个最大的qk，也就是最大的action value

例子

通过不断地迭代，就会选择到所有action中最好的一个action，也就是一个最优的Policy

Policy iteration(策略迭代)

步骤：

• Policy evaluation：通过首先给出Policy，然后使用贝尔曼公式计算对应的state value，这样的一个过程就叫做Policy evaluation

• Policy improvement：对上一步求解出来state value做一个优化问题，从而得到一个新的，并且比之前更好的Policy

Q1：怎么做Policy evaluation

A1：通过使用贝尔曼方程，用求逆矩阵或者迭代的方法来求出在这个策略下的state value

Q2：为什么我得到的新策略一定比老策略好？

Q3：为什么迭代算法一定能找到一个最优的策略

每次迭代过后的state value值都会更大，这个值大到最后就会逐渐的趋近于收敛，也就是我们最优解

Q4：Policy evaluation与Value iteration的关系

具体实现

依然是先设定一个state value，然后进行不断地迭代，最终求解出实际的state value

实际上就是贝尔曼最优方程之中的求最优解的那一步

也就是先计算出一个状态下的所有action value，然后选取一个最大的action value，然后将策略更新为选取那个action的概率为1

例子1

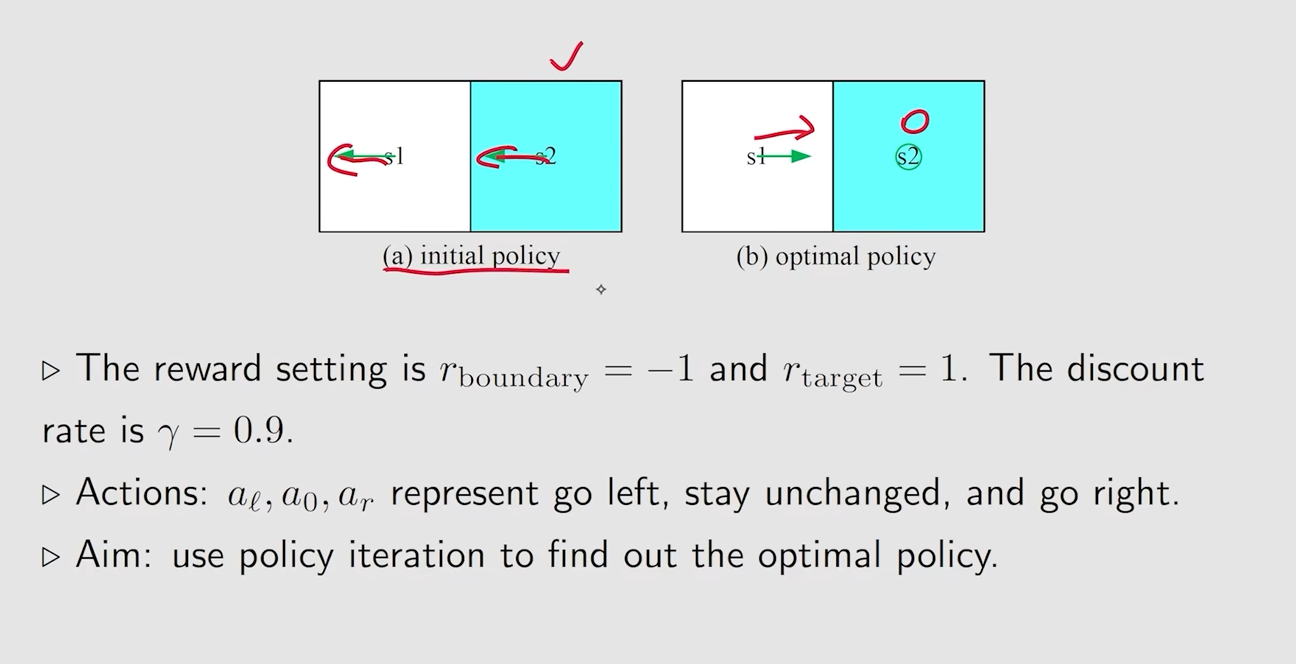
例子2

当周围没有状态到达目标区域时，更新也无法到达目标区域，当周围有状态到达目标区域时，就会逐渐更新从而到达目标区域

小总结

Value Iteration是不断的迭代state value，使得最终的state value进行收敛，从而得到最优策略 Policy Iteration是不断的迭代Policy，使得Policy不断收敛，从而得到最优策略

Truncated policy iteration

在第四步时：

在策略迭代中，求解需要进行迭代，依然是相当于求一个贝尔曼公式

在值迭代中，可以进行直接求解，因为没有未知数

如果设置在策略迭代时的最开始的VΠ1 = V0(值迭代的初始预估值)

那么第一次迭代后的VΠ1实际上就等于了V1

所以实际上策略迭代与值迭代就只有一步不相同，就是在上面第四步，在这个第四步中，值迭代可以看作就是策略迭代中的第一步

而策略迭代实际上就是迭代了无穷次之后所计算出来的VΠ1

如果用一般化的方法来描述这个不走，从而对于使用中间步骤的VΠ1的方法，我们称之为truncated police iteration

伪代码

与策略迭代是一样的伪代码，只是在判断条件上变成了判断是否达到了所设定的迭代次数，从而判断是否继续迭代下去

无论如何随着迭代都会逐渐的增大state value，所以就算只进行有限步，也是在逐渐收敛的过程中，只是说收敛程度不同

• Policy iteration算法因为在中间步骤就已经迭代到了最优，所有收敛速度会是最快的

• 相对的，Value iteration算法因为在中间步骤只做了第一步收敛运算，所以收敛速度是最慢的

• 而 Truncated police iteration的收敛速度位于两者中间，取决于迭代步数多少的设置

总结