Mean estimation

• 首先有一个随机集合X，希望求这个集合的期望

• 对集合中进行随机采样

• 根据求平均的方法求出来他的期望

方法一是指等全部采样完成之后，再进行一个mean的计算，这样做的问题是在于要等待采样结束，需要很长的时间

方法二则是每次采样结束都进行一个mean的计算，然后进行迭代，这样的效率会更高

这里的目的是为了建立起Wk与Wk+1之间的关系

这是一个求平均式的迭代式的算法，也就是上面的方法二，这样就不需要等到采样全部完成再进行求平均数

而且每一次求出Wk都会用到其他任务中去，虽然最开始的Wk和真实值的关系不是很大，但是随着数据的增加，就会越来越接近真实值

Robbins-Monro 算法

Stochastic approximation(SA)

SA可以不需要直到方程的表达式等信息，依然可以进行求解

Robbins-Monro 算法

随机梯度下降与mean estimation 算法都是属于特殊的RM算法

对于最优化问题，通常是找到函数的极值，也就是函数的梯度(暂时理解为斜率)等于0的情况，则是一个函数达到最大或者最小的必要条件

如何求解这个梯度等于0的情况？

当知道表达式的时候，可以用一些特定的算法进行梯度的计算

如果什么都不知道的情况下怎么计算呢？

类比于神经网络

算法说明

Wk是第k次的估计，而Wk+1是第k+1次的估计，这个估计就等于了Wk减去了一个ak g(Wk,nk),实际上这个g(Wk,nk)就是一个带有噪音的梯度

这里的梯度实际上就是一个黑箱

中心思想始终还是，没有模型的话，我们就得使用数据，这里的模型实际上就是表达式

收敛性分析

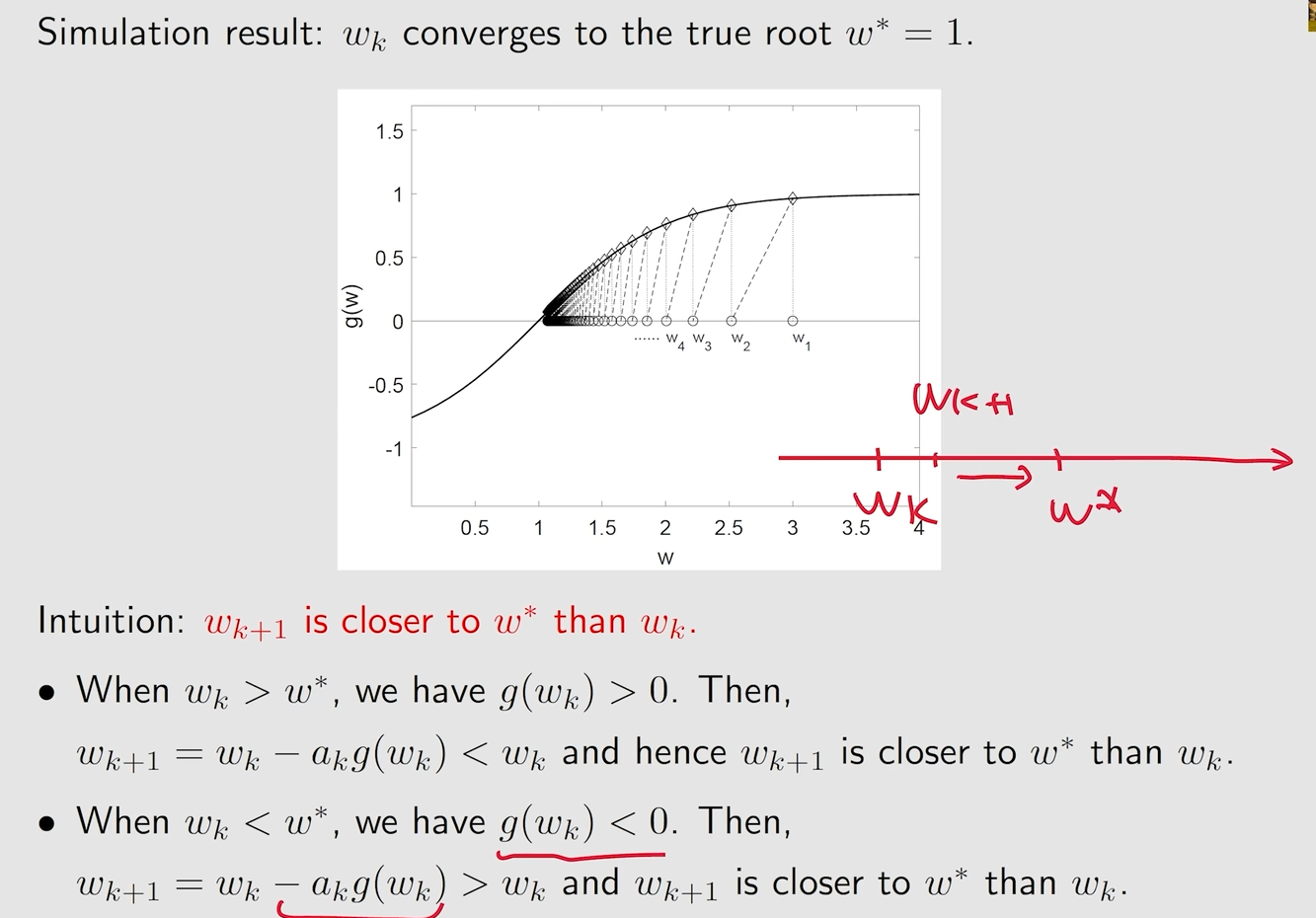
Wk+1始终比Wk距离W*更近

条件一：g必须是有界的，且g需要是单调递增的，才能表明g有一个零点

条件二

当右边趋向于0的时候，坐标也就是趋向于0的，也就是趋向于收敛的

应用

Stochastic gradient descent(SGD)

算法描述

通过优化W，让J(W)达到最小就是SGD的目的

方法一(梯度下降)

最小化一个函数的方法是梯度下降，如果想要最大化一个函数，需要使用梯度上升

方法二(批量梯度下降)

每一次去采样Wk的时候都要采样N次，还是很困难

方法三(随机梯度下降)

相当于直接采样一次的批量梯度下降，只用采样一次的Wk来进行梯度下降

例子与收敛性

例子

这个地方相当于E[f(w,x)]中的fx是w到X之间的距离

问题一：为什么最优解W*是等于E[X]？

J(w)要达到最小值，相当于对它求梯度，要等于0

则相当于E[w-x]=0,则w=E[x]

收敛性

相当于只用一个随机采样的值取替代一个期望

收敛过程中的行为

虽然平均值的初始估计值离真实值很远，但SGD估计值可以快速接近真实值的邻域。

当估计值接近真实值时，它表现出一定的随机性，但仍逐渐接近真实值。

问题

MBGD,BGD,SGD

BGD就是对一个分支全部采样完，然后再求E

MBGD就是选取部分采样后，求E

SGD就是只采样一次，求E

• MBGD与BGD和SGD的比较:与SGD相比，MBGD的随机性更小，因为它使用了更多的样本，而不是SGD中的一个样本。

• 与BGD相比，MBGD不需要在每次迭代中使用所有的样本，使其更加灵活和高效。

• m = 1时，MBGD变为SGD。

• 如果m = n，严格来说MBGD不成为BGD，因为MBGD使用随机获取的n个样本，而BGD使用所有n个数字。特别是，MBGD可能多次使用{xi}=1中的值，而BGD只使用每个数字一次。

例子

总结