5-蒙特卡洛方法(Monte Carlo)
笔记/强化学习

5-蒙特卡洛方法(Monte Carlo)

理论支撑(大数定理)

理论支撑(大数定理)

image-20231221102626335

Simplest MC-based RL algorithm

将Policy iteration改为model-free的(核心点)

对于Policy iteration来说，怎么样得到新的策略Π，就是找到这个qΠk的最大值

最核心的量就是这个qΠk，也就是这个action value

如何求解qΠk(action value)

方法一：依赖于模型的算法

实际上就是一个value iteration的方法

方法二：不依赖于模型的方法

action value最初的定义实际上就是，在状态s时，take action a，然后得到一个return，然后这个return是一组随机数据，然后对他们求加权平均(期望)

那么这就变成了一个求期望的问题，对于求期望的问题，就可以使用蒙特卡洛的方法来做

MC-basic的定义

image-20231221103620451

  1. 首先从状态s take action a 后following policy Πk，得到一条episode

  2. 然后选取这跳episode中的一个discounted return(因为初始动作确定，对于后续的状态和奖励也会因为随机性而不同，因为没有模型)

  3. 这个discounted return实际上就是这个action value中的一次采样(experience)

  4. 然后求得很多个discounted return之后，就可以通过大树定理求解出action value

image-20231221110514276

Simplest MC-based RL algorithm总体来说和策略迭代是一样的，区别就在于第一步求解action value的时候，因为没有模型，所以直接使用蒙特卡洛的方法去进行采样，然后求解出action value(Policy evaluation) 然后选取一个最大的action value，然后将策略更新为选取那个action的概率为1(Policy improvement)

image-20231221111157199

伪代码：

  • 对每一个state的每一个action都进行一个action value的计算(使用MC-based)

  • 然后选取一个最大的，然后将策略更新为选取那个action的概率为1

MC-basic的例子

image-20231221111720261

image-20231221111735759

image-20231221111841134

image-20231221111911614

image-20231221111935991

MC-basic的例子2

image-20231221125051321

image-20231221125140135

如果episode的长度为1，实际上就只探索了一个四联通区域，所以只有距离目标最近的几个state能选取到正确的action

image-20231221125440007

image-20231221125528296

image-20231221125556327

  • 当episode length很短的时候，就只有靠近了目标的几个状态会选择到非零的state value

  • 当episode length加长时，随着长度的增加，越来越远的状态也会得到state value

所以episode length需要选择足够充足的长

MC Exploring Start

用于将MC-basic变得更加的高效

image-20231221131839333

把每一次的S与a设定为一次Visit，比如上面的S1与a2就是一组Visit

在MC-basic中所使用的策略交错initial-visit，也就是只考虑s1，a2，用剩下的return(s2,a4、s1,a2、s2a3等)来估计s1，a2的action value

这样做的问题是浪费了这个episode中的很多数据

image-20231221134639582

不单单用来估计s1，a2，在s1,a2后面的部分的数据可以用来估计s2,a4

first-visit method: 如上图所示，s1,a2出现了两次，那么第一次估计出结果后，就不会再使用第二次进行估计

every-visit method: 在每一次s1,a2出现时都进行重新估计

image-20231221140458933

在MC-basic方法中，等待求出所有的episode的return之后再进行加权平均然后再优化

但是效率更高的的方法是，在得出一次episode的return之后，就直接开始求action value，然后就直接开始做优化

image-20231221140730409

在GPI中，就是不断地进行策略评估和策略优化的转换，没得到一次episode就会得到一个return然后直接开始求action value，然后进行优化

image-20231221140911566

t是从后往前计算是为了提高计算效率

  1. 对每一条的episode，先初始化g=0

  2. 然后计算这个episode中每一步的return

  3. 然后action value就是这些return的加权平均

  4. 然后再通过选取最大的一个action value的那个action作为Policy来改进策略

image-20231221141956978

  • 理论上，只有充分探索了每个状态的每个动作值，我们才能正确地选择最佳动作。相反地，如果一个行动没有被探索，这个行动可能恰好是最优的，因此被错过了。

  • 在实践中，探索起步是很难实现的。对于许多应用程序，特别是那些涉及与环境的物理交互的应用程序，很难从每个状态-动作对开始收集情节。

MC Epsilon-Greedy算法

soft policy

image-20231221142256863

可以通过几个很长的episode可以将每个state action 都覆盖到

image-20231221142550478

给最好的action的概率很大，而其他的action也给概率，但是概率相对较小

image-20231221174241903

exploitation的含义是指，对于一个state上始终选取目前action value最大的那个action，用于更充分的利用这个action value

exploration的含义是指，对于一个state上有可能不去选取action value最大的那个action，这样用于更充分的去探索其他action，因为其他action有可能在之后的探索中会变成最大的action value

这里的可能性就由Epsilon决定，

  • 当Epsilon越接近于0，则算法更倾向于一直利用最大的那个action

  • 当Epsilon越接近于1，则算法更倾向于去探索其他的action

具体定义

image-20231221174759298

image-20231221174835124

与MC Exploring Start算法基本是一样的，区别就在于Policy improvement这一步中，MC Epsilon-Greedy算法将会给每一种action都有一些概率，而不是只给action value最大的那个值的概率直接为1

image-20231221175119490

这个地方要用every-visit，因为有时候有些visit被访问了很多次，如果我们只用一次进行估计，就会有些浪费

例子

image-20231221175305562

image-20231221202605982

例子

image-20231221202659050

image-20231221202748602

image-20231221202839670

优点：具有较强的探索能力，不需要对开始条件有要求，也就是说，我们可以从任意一点开始，然后选取一个或者几个点就可以探索完所有的action，并且得出一个相对最优的Policy

缺点：为了上面的优点，所牺牲的部分实际上就是Policy的最优性，所以这样最后得到的Policy实际上不是最优的

最优性

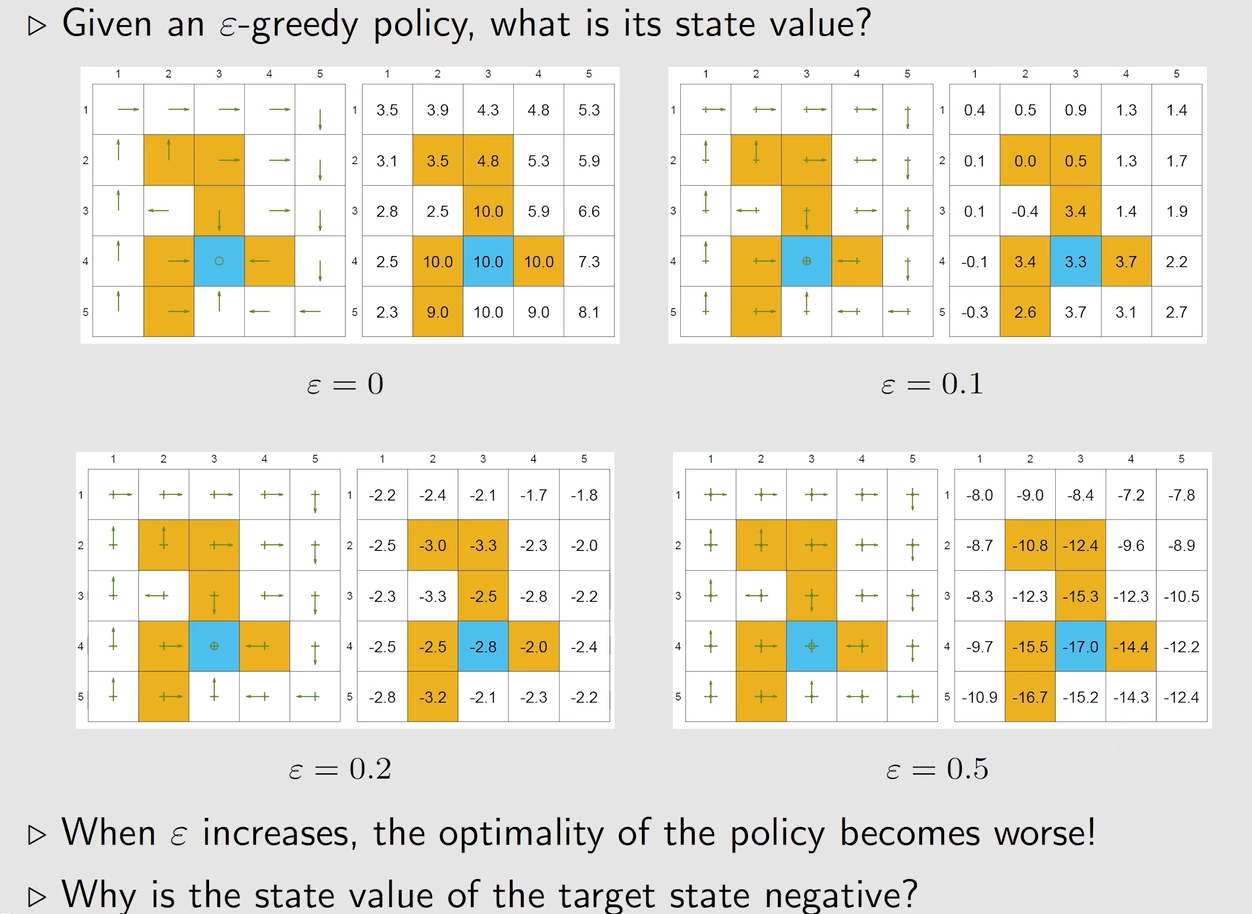
image-20231221203752131

如果Epsilon过大，会逐渐降低最优性

image-20231221204000450

如果想要得到一个相对好的Policy，一个做法就是在最开始时增加Epsilon用于探索，然后逐渐逐渐的降低Policy，使得最后可以得到一个最优的确定策略

总结

Comment