1-强化学习基本概念
笔记/强化学习

1-强化学习基本概念

在一个网格地图中进行强化学习的理解，网格分为四种情况，分别为可通行，障碍物，目标位置与边界 在移动时可以进行四通移动，也就是上下左右移动 目的是为了找到一个好的路径到达目标位置

image-20231219194001233

在一个网格地图中进行强化学习的理解，网格分为四种情况，分别为可通行，障碍物，目标位置与边界

在移动时可以进行四通移动，也就是上下左右移动

目的是为了找到一个好的路径到达目标位置

怎么理解好的呢？尽量的避免障碍物，转弯与进入边界

state(状态)

image-20231219195014808

State其实就是指agent在环境中的状态

在这张图中，State就相当于是一个location（S1，S2，S3，S4 ...），而State space就是这些location的集合

Action(行动)

image-20231219195341128

在每一个State都会有一些可能的Action

比如在这个例子中，Action就是指在一个State(方格)中，可能行动的方向，比如a1,a2,a3,a4,a5分别对应了五种不同的可能性

所有这些可能性的集合就叫做Action space of a state，所以在这个地方A(si)代表了A是si的一个函数，因为对于每一个si都会有不同的A

state transition(状态转移)

image-20231219195955377

当采取action时，agent会从一个state转移到另一个state，这个就叫做state transition

比如这个地方，当S1采取了a2(向右走)就会到达S2，当采取a1时则会留在s1，因为向上是边界，只能保持在原地

state transition 定义了与环境的交互

image-20231219200453873

对于障碍物区域，进行设置为，当state走入障碍物时，可以走进去，但是会被弹出来

image-20231219200613384

可以进行用表格表示一个state transition，但是这个情况只能表示一个确定的状态，也就是当S1选取不同的action之后，得到的下一个状态是确定的

State transition probability(状态转移可能性)

image-20231219200857654

这个地方，可以看为，我目前在S1，take action a2，走到S1的概率为1，走到Si的概率为0，因为在这个位置是一个绝对的情况

也就是

P(s_i|s_j,a_k)


的意思就是说，在sj的位置上take action ak到达si的概率为P

Policy(策略)

image-20231219201429490

Policy用于告诉agent，在哪一个state时take 哪种action

比如在图中所有的绿色箭头和圆圈就是Policy

image-20231219201630099

Π在强化学习中指的就是条件概率

比如在这个地方

Π(a_i|s_j)


就是代表了在状态sj时选取action ai的概率为多少

在一个状态下所有的概率之后应该等于1

image-20231219202005207

对于一个不确定情况的例子，如上图所示

image-20231219202123250

同样的，可以用表格对于Policy的概率进行表示

Reward(奖励)

agent在采取了一个action之后，可以得到一个Reward

如果Reward为正，则代表鼓励采取这种action

如果为负，则要对采取这种action进行惩罚(punishment)

image-20231219203101548

Reward实际上是一种human-machine interface，也就是我们和agent就行交互的一种手段，通过设置不同的reward进行引导，让agent实现我们的目标

image-20231219203342467

对于

p(r=-i|s_j,a_k)


这个实际上代表了在sj的状态下，take action ak得到reward为-i的概率为P

Reward始终取决于当前的state所take的action，而和下一个状态无关

Trajectory and Return

image-20231219203825392

Trajectory实际上是一个state-action-reward所形成的一个链

每一个Trajectory都带有一个return，也就是所有在这个trajectory中所有的reward加起来，就是总的一个return

return就是一个用于比较Trajectory好与坏的标准

Discounted return

image-20231219204720100

在target时，会一直加+1+1+1最终发散掉，所以我们需要找到一个方法避免一个无限的reward

image-20231219204844095

这时候就要引入一个在[0,1]的discount rate γ ，然后在每一个return的前面都乘上γ的幂乘，就可以让最后的结果变得很小从而不至于发散，并且可以引导函数通过最小的步数到达终点（因为越靠前则权重越大）

Episode

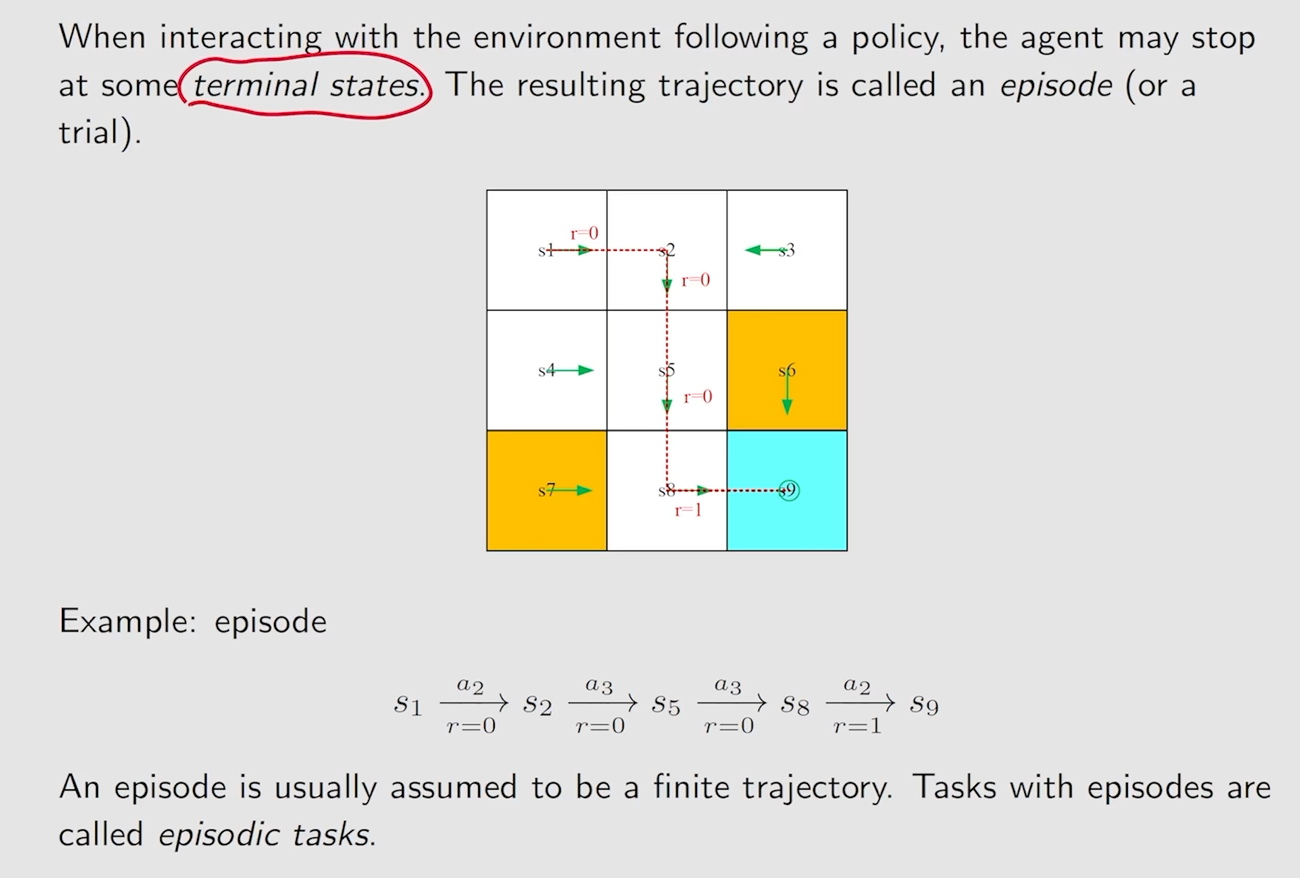
image-20231219210221377

当遵循策略与环境交互时，代理可能会在某些终端状态停止。由此产生的轨迹被称为一个Episode(或试验)。

实际上来说就是环境中从起点到终点的一条总的trajectory

Markov decision process(MDP)

Set：

  • State：所有状态的集合

  • Action：对于每所有State的所有action的集合

  • Reward：对于每一个action所能获得reward的集合

Probability distribution：

  • State transition probability：在状态s选择action a之后到达s‘的概率

    p(s'|s,a)

  • Reward probability：在状态s选择action a之后获得reward r的概率

    p(r|s,a)

Policy

在状态s，选择action a的概率是多少

Π(a|s)


Markov property

image-20231219211722158

不考虑历史，只考虑当前状态和当前所take的action

Markov decision process(MDP)中的

Markov：代表与历史无关的性质

decision：代表需要选取Policy

process：拥有Set和Probability distribution

image-20231219212050076

右边的这个图代表的是markov process(MD),因为在这个图中的policy是没有确定的

Comment