CLF-CBF解析
优化问题

CLF-CBF解析

这篇文章介绍了作者在学习MPC-CBF小车避障算法之前，对相关前置知识DCLF-DCBF的总结，包括Lyapunov理论的基本思想、稳定性分析、控制仿射系统、控制李亚普洛夫函数和指数稳定CLF等内容。

写在前面

最近想学习一下MPC-CBF用来做小车的避障，所以在学习MPC-CBF之前准备先学习一下关于他的前置知识，也就是DCLF-DCBF，这里是根据伯克利课程的内容进行的一个总结。

Lyapunov theory(李亚普洛夫理论)

基本思想

Lyapunov theory的基本思想就是通过设计一个特殊的函数，称为Lyapunov函数(类似于能量函数)，这个函数用来度量系统状态的“能量”或“势能”。在平衡状态下，Lyapunov函数通常取最小值。

如果Lyapunov函数随着时间的推移不断减小（即系统状态的“能量”不断降低），那么系统就会趋向平衡状态，因此系统是稳定的。反之，如果Lyapunov函数增大或不减小，那么系统可能是不稳定的。

稳定性分析

首先我们先定义一个系统为​\dot{x}=f(x),这个系统拥有一个初始点​x_0和一个稳定点​x_e我们需要验证这个系统最终是否会到达稳定点​x_e，所以我们要设计一个Lyapunov function(李函数) ​V(x)：

V(x)\\\mathbf{s.t.} V(x_{e})=0,V(x)>0 \ \mathrm{for} \ x\neq x_{e},\\\dot{V}(x)=\frac{\partial V}{\partial x}f(x)<0 \ \mathrm{for} \ x\neq x_{e}
  • ​ V(x_{e})=0,V(x)>0 \ \mathrm{for} \ x\neq x_{e} 表示了稳定状态下的​V(x)为0，并且在非平衡状态下​V(x)恒大于0
  • ​\dot{V}(x)=\frac{\partial V}{\partial x}f(x)<0 \ \mathrm{for} \ x\neq x_{e}
    • ​\dot{V}(x)<0 \ \mathrm{for} \ x\neq x_{e} 说明了在​x\neq x_{e}这个区间中​V(x)的值是在不断减小的
    • ​\dot{V}(x)=\frac{\partial V}{\partial x}\frac{dx}{dt} = \frac{\partial V}{\partial x}f(x)<0 \ \mathrm{for} \ x\neq x_{e}

对于这个系统​\dot{x}=f(x)，如果能够找到一个满足上述条件的Lyapunov函数​V(x)，那么可以证明系统在​x_e处是渐近稳定的并且状态​x所构成的集合，可以称为一个**不变集(Invariance set)**也就是说，如果系统状态 ​x 受小扰动偏离平衡点 ​x_e，它将随着时间逐渐返回到平衡点，而不会偏离得更远。

不变集合：如果存在一个集合​C被称为不变集合，则意味着，如果系统的初始状态​x(0)在这个集合内，那么随着时间的演化，系统的状态​x(t)将始终保持在这个集合内。换句话说，系统一旦进入这个集合，它就不会离开。

Nagumo’s Invariance Principle

Nagumo’s Invariance Principle是一种在动力系统中分析不变集(invariant set)的方法。它用于判断一个集合是否为一个不变集

举例来说，首先我们依然先定义一个系统为​\dot{x}=f(x),Nagumo’s Invariance Principle的作用就是评估这个系统的轨迹是否会停留在一个我们所希望的某个区域内,如图1中的蓝色区域

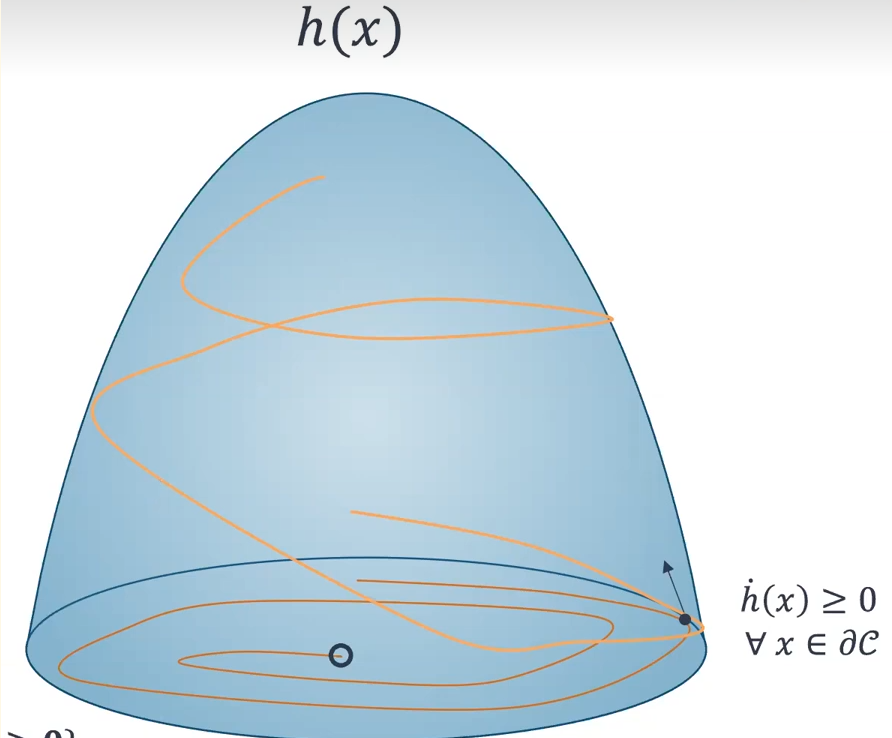
image-vgjd.png

图1 Nagumo’s Invariance Principle的图像

具体的，在我们定义一个动力系统，描述为

\dot{x}=f(x)

其中，​x是系统的状态向量，​f(x)是描述系统动态的向量场。给定一个函数​h(x),我们可以定义(或者说找到)一个集合​C，如下所示：

C=\{x\mid h(x)\geq0\}

这个集合​C包含了所有满足​ h(x)\geq0的点。并且这个集合的边界为：

\partial C=\{x\mid h(x)=0\}

Nagumo’s Invariance Principle 的定义也就是：如果在集合​C的边界​\partial C上，向量场的方向始终不离开集合​C，那么​C就是一个不变集。

具体来说，如果对于​x\in\partial C，

\dot{h}(x)=\frac{\partial h(x)}{\partial x}f(x)\geq0

那么集合​C是一个不变集，这也就意味着，如果系统的初始状态位于集合​C内，那么它就将始终停留在集合C内

这里其实就可以理解为，对于系统的动态向量场中的如果能找到这个集合​C，那么如果系统的初状态在集合​C中，系统就会始终保留在集合​C内

Dynamic-Control Affine System

一般非线性控制系统

我们首先列出一般非线性控制系统的动力学表达式为：

\dot{x}=F(x,u)

其中：

  • ​x\in\mathbb{R}^n表示了系统的状态
  • ​u\in\mathbb{R}^m表示了控制输入
  • ​F(x,u)是系统的动力学函数，描述了状态​x的变化率(​\dot{x})如何依赖于当前的状态​x和控制输入​u

对于系统轨迹的存在性与唯一性的条件：

  • 如果​F对​x是Lipschitz连续的，并且对​u是连续的。
  • 如果控制输入​u(t)对时间​t是分段连续的，那么对于给定的初始状态​x(t_0)=x_0,我们可以保证系统的动力学轨迹​x(t)存在且唯一的

Control Affine System(控制仿射系统)

Control Affine System(控制仿射系统)是一种特殊形式的控制系统，其状态方程是关于控制输入​u(t)线性的，标准形式为：

\dot{x}=f(x)+g(x)u

其中：

  • ​x是系统的状态向量
  • ​u是控制输入向量
  • ​f(x)是仅依赖于状态​x的非线性函数，描述了无控制输入的情况下，系统的状态变化
  • ​g(x)是与控制输入相关的矩阵函数，描述了状态与控制输入​u之间的关系

对比传统状态空间方程和控制仿射系统之间的关系

仿射系统和状态空间方程是一种包含关系，可以说仿射系统是一种特殊的状态空间方程，并且我暂且理解(不确定对错)为对于一个系统来说，我们可以将其定义为为仿射系统和非仿射系统两种，这两种的区别是对于控制输入​u上的线性或非线性特性的划分。

  • 例子1：
\dot{x}_1=x_2 \\ \dot{x}_2=-x_1+u

对于这个系统而言，控制输入​u以线性的形式影响​\dot{x_2}，所以这是一个仿射系统。

  • 例子2:
\dot{x}_1=x_2 \\ \dot{x}_2=-x_1+u^2

对于这个系统而言，控制输入​u以线性的形式​u^2影响​\dot{x_2}，所以这是一个非仿射系统

这还是我第一次看到Control Affine System这个东西，可能是因为半路出家的缘故，这边大概猜测一下，之前一直没有看到这个概念是因为目前大多数情况下所处理的系统都会处理成仿射系统来使用，所以大多数情况下已经是一个前置概念了？

Control Lyapunov Function(CLF) 控制李亚普洛夫函数

Asymptotically stability CLF 渐近稳定CLF

对于Lyapunov Function来说，是判定系统在某个区域内的稳定性，如果在某个区域内，系统是稳定的，从这个区域的任意为止开始，状态都会回到稳定点，如图2所示

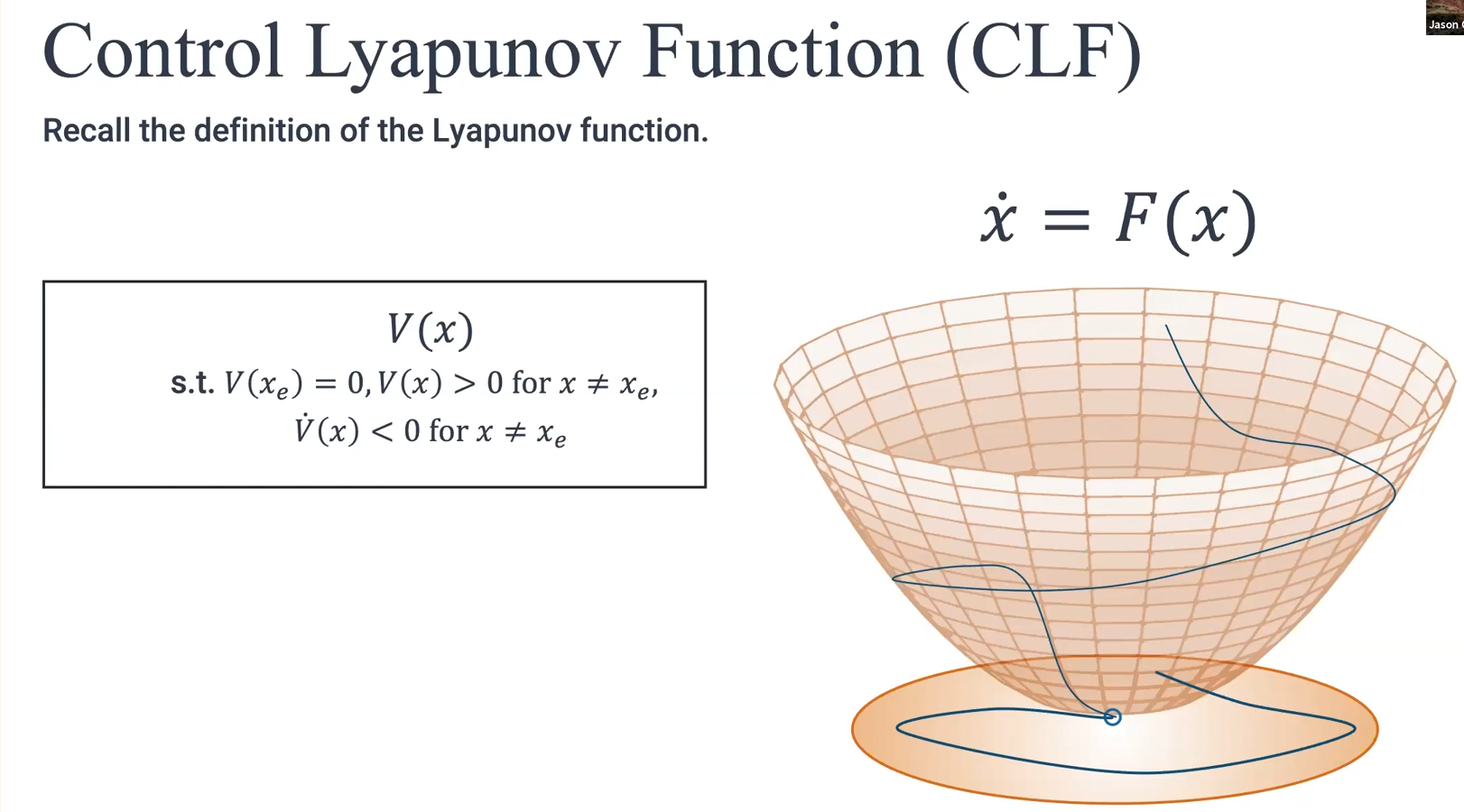
image-fmpw.png

图2 Lyapunov Function的图像

当我们在图2得系统中引入了控制量后，我们就可以将Lyapunov Function改写为Control Lyapunov Function，如图3所示

image-qcdm.png

图3 Control Lyapunov Function的图像

这里就是意味着，存在一个控制信号​u使得​\dot{V}在​x\neq x_{e}时始终小于0，这样做的目的是为了扩大李雅普诺夫函数在系统中的作用域，从而使系统在更大范围内稳定(或者说在我们感兴趣的区域内稳定？)

具体的，说明一下CLF的满足条件：

  • ​V(x)是一个从状态空间​\mathbb{R}^n到实数​\mathbb{R}的连续可微函数
  • ​\Omega_c:=\{x\in\mathbb{R}^n:V(x)\leq c\}
    • ​\Omega_c是又函数​V(x)定义的一个子集，表示​V(x)不超过某个常数​c的状态集合。这个集合是有界的，意味着系统状态​x被限制在某个有限范围内
  • ​V(x)>0\quad\text{for all} \quad x\in\mathbb{R}^n\setminus\{x_e\},V(x_e)=0
    • 这表明​V(x)对于所有状态​x都是正的，除了在平衡点​x_e处，那里的​V(x)为0。这个条件类似于Lyapunov Function的性质，用于保证平衡点​x_e是稳定的候选点
  • ​\min_{u\in U} \dot{V}(x,u)<0\quad\text{for all}\quad x\in\Omega_c\setminus\{x_e\}
    • 这个条件要求存在一个控制输入​u，使得任何​x状态下，​V(x)相对于时间的导数​\dot{V}(x,u)都是负的。这意味着系统状态​x随着时间的推移会向着降低​V(x)的方向演化，即趋向于平衡点​x_e，从而确保系统的渐近稳定性

如果以上的条件全部满足，则​V(x)被称为一个Control Lyapunov Function，且​\Omega_c是吸引域(Region of Attraction，ROA)。这意味着对于所有初始状态在​\Omega_c中的状态​x_0存在一个控制输入​u(t),使得系统状态​x(t)会逐渐稳定到平衡点​x_e(asymptotically stability 渐近稳定性)

接下来让我们着眼于CLF中与控制量​u有关的部分，也就是​\dot{V}(x,u),我们可以将其写为以下形式：

\begin{aligned} \dot{V}(x,u)& = \nabla V(x)\cdot\dot{x} \\ &=\nabla V(x)\cdot f(x)+\nabla V(x)\cdot g(x)u \\ &=L_fV(x)+L_gV(x)\boldsymbol{u} \end{aligned}

其中，​L_{p}q(x):=\nabla q(x)\cdot p(x)被称为Lie derivative operator(李导算子)，用于将公式进行简化，并且改写为形似仿射系统方程的形式，这将会代带来很多便利

Exponentially stabilizing CLF 指数稳定CLF

对于渐近稳定CLF，我们关注的是系统最终会收敛到平衡点，但并不考虑收敛的速度，在这种情况下，​\dot{V}(x,u)只是小于0，着意味着​V(x)随时间衰减，从而表明系统状态​x(t)最终会收敛到平衡点​x_e。但这种收敛速度是可快可慢的，系统可能会经过一个很长的时间才会到达平衡点，这个时间可能不是我们所期望的。

因此我们引入了Exponentially stabilizing CLF，指数稳定CLF将进一步的要求系统不仅仅是收敛到平衡点，而且设定了一个最低的速率(通常是指数速率)进行收敛，也就是说我们将限定收敛速度最慢也得是指数速率进行收敛

接下来给出具体的定义与条件：

首先，给定一个李亚普诺夫函数​V(x)，其必须满足以下条件

  • 连续可微(continuously differentiable): ​V(x)在其定义域内是可微的，而且导数是连续的。
  • 正定函数(positive definite): ​V(x)对所有的​ x\neq x_{e}是正的，而在平衡点处​ x= x_{e}为0
  • 辐射无界(radially unbounded): ​V(x)随着​x的距离从平衡点​x_e增大而趋向于无穷大

如果存在一个常数​\lambda>0使得对于某些控制输出​u \in U：

\min_{u\in U}\dot{V}(x,u)+\lambda V(x)\leq0

那么这个​V(x)就是一个Exponentially stabilizing CLF (ES-CLF)，如图4所示

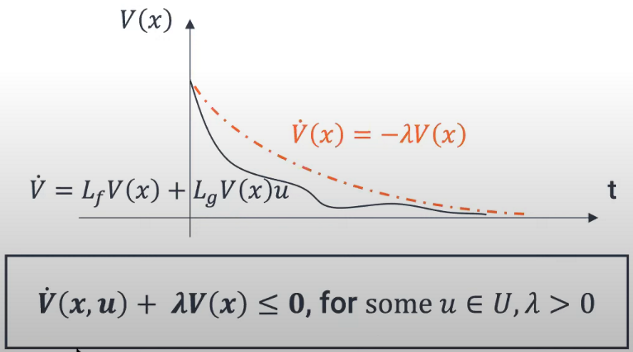
image-ndka.png

图4 ES-CLF的图像

其实也就是​\dot{V}(x,u)\leq- \lambda V(x)，其中​-\lambda V(x)代表的是指数下降速率，也就是我们需要比指数下降速率更快

CLF-QP

那对于上面的ES-CLF而言，我们所需要做的，就是找到一些控制量​u来使得不等式​\dot{V}(x,u)\leq- \lambda V(x)成立，那么如何找到呢？

这个时候就要引入Quadratic programming(QP) 二次规划求解器了，因为CLF约束对于控制量​u来说是线性的，具体的，我们可以将约束条件写成如下形式：

L_fV(x)+L_gV(x)u+\lambda V(x)\leq0

我们可以看到，在这个约束条件中，控制输入​u仅出现在了线性项​L_gV(x)u中，也就证明了这个约束对于​u来说是线性的，所以我们就可以以​u作为目标函数来写出QP的公式如下：

\begin{align*} \text{argmin}_{u, \delta} & \quad (u - u_{ref})^T H (u - u_{ref}) + p \delta^2 \\ \text{subject to:} & \quad L_f V(x) + L_g V(x) u + \lambda V(x) \leq \delta \\ & \quad u \in U \end{align*}

其中：

  • ​u是控制输入
  • ​\delta是松弛变量
    • 这里引入松弛变量的目的是有时候可能没法找到满足不等式的控制量​u，引入松弛变量是为了保证优化问题是有解的
  • ​L_f V(x) + L_g V(x) u + \lambda V(x) \leq \delta CLF的约束项
  • ​u \in U 控制量的约束项

通过求解这个QP问题，我们就可以找到一个满足ES-CLF的控制量​u使得系统始终保持在吸引域

\Omega_c

内并且按照期望的速率达到稳定点​x_e(感觉这个理解还是存在问题，先写着，之后确定问题再来改)

Control Barrier Function(CBF) 控制障碍函数

终于写到了最后的部分，也就是真正拿来保证小车运行过程与障碍物之间保持距离的CBF部分，按照概念来说，CBF是一种确保系统状态始终保持再一个安全集合​C内的方法，可以类比于CLF，都是通过引入一个控制量​u来使得系统停留在某个集合内。

具体的定义：

设CBF为​B(x)：​\mathbb{R}^n\to\mathbb{R}是一个连续可微的函数，它定义了一个集合​C：

C=\{x\mid B(x)\geq0\}

并且，在这个定义中：

  • ​B(x)>0定义了安全区域​C，即系统状态需要保持在​C内。
  • ​B(x)=0表示集合​C的边界​\partial C，即状态正好位于边界处，并且此时的​\dot{B}(x,u)要大于0
  • ​B(x)<0则表示状态位于​C的外部，是我们需要避免的情况

通过类比CLF的方法，我们可以画出CBF的图像，如图5所示

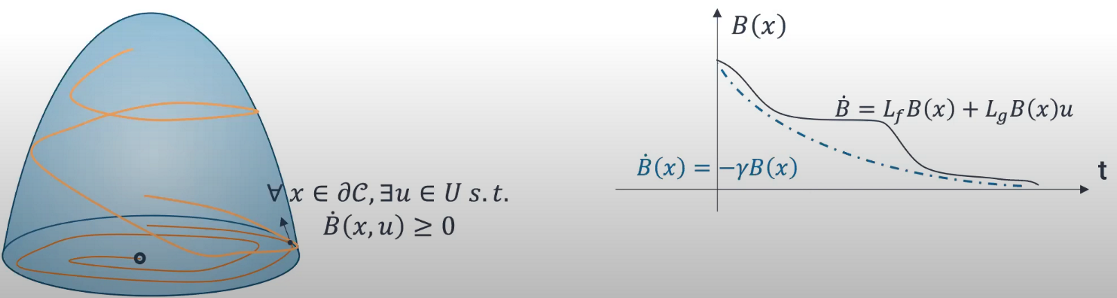
image-piyo.png

图5 CBF的图像

拿小车与障碍物的例子来说明这个地方，可以理解为，因为在CBF中，​B(x)需要恒定的大于等于0，所以这里的​B(x)所代表的实际上是小车与障碍物之间的距离，而​\dot{B}(x)代表的是小车与障碍物之间的距离变化率，​-\gamma B(x)是一个反馈项，用于调整"控制力度"，具体的，根据公式：

\sup_{u\in U}\left[L_fB(x)+L_gB(x)u+\gamma B(x)\right]\geq0
  • ​L_fB(x)+L_gB(x)u是关于状态和控制输入的线性组合，表示了在给定控制输入​u下​B(x)的变化率
  • ​\gamma B(x)是一个附加项，用来调节系统状态​x对距离函数​B(x)的反馈

当小车（系统）靠近障碍物（即​B(x) 变小）时，​-\gamma B(x)变得更加显著。因为γ是一个正系数，这意味着在​B(x)变小的情况下,​-\gamma B(x)会变得更加负，这迫使​u的影响更强烈，以确保​B(x)不会继续减小到负值（即系统不会进入不安全区域，通过调节​\gamma的值可以让这种"控制力度"进行增加或减小

CLF-CBF

其实结合上面的CLF-QP以及CBF之后，就可以很简单的得出CLF-CBF的公式，也就是在CLF-QP中加上CBF的约束

\begin{align*} \text{argmin}_{u, \delta} & \quad (u - u_{ref})^T H (u - u_{ref}) + p \delta^2 \\ \text{subject to:} & \quad L_f V(x) + L_g V(x) u + \lambda V(x) \leq \delta \quad \text{(CLF Constraint)} \\ & \quad L_f B(x) + L_g B(x) u + \gamma B(x) \geq 0 \quad \text{(CBF Constraint)} \\ & \quad u \in U \quad \text{(Input Constraint)} \end{align*}

当考虑了多个障碍物时，对每一个障碍物都要加上CBF约束，例如CBF1,CBF2...一类的

总的来说对于这个CLF-CBF，CLF负责保证了系统的稳定性，而CBF则负责保证了系统的安全性

参考

控制障碍函数解析

控制障碍函数课程

Comment