✨ 背景介绍
在路径规划中,B样条(B-Spline)以其光滑、连续、可微的优势广泛应用于轨迹表示。而优化控制点的位置,是提升轨迹质量的关键一步。
本篇专注于一种重要的代价项 —— 基于 ESDF(欧几里得距离场)地图 的避障代价,并深入解析其 数学推导、可导性、代码实现与可视化理解。
1️⃣ 问题定义:控制点形式的 B 样条轨迹
轨迹定义为一条均匀 B 样条曲线:
\mathbf{x}(t) = \sum_{i=0}^{n} \mathbf{P}_i B_{i,k}(t)
其中:
- \mathbf{P}_i \in \mathbb{R}^2:控制点(优化变量)
- B_{i,k}(t):B样条基函数(阶数 k)
通过优化 \mathbf{P}_i,我们得到一条柔顺、安全、避障的轨迹。
2️⃣ ESDF 地图与安全代价项
🧱 什么是 ESDF?
- ESDF(Euclidean Signed Distance Field)是一张二维地图
- 每个栅格存储 到最近障碍物的欧几里得距离
\text{distance\_map}(i, j) = d(i, j)
🔺 安全代价项定义
若控制点 \mathbf{P}_i = (x_i, y_i) 距离障碍太近(即 d(x_i, y_i) < d_0),将施加惩罚:
J_{\text{obs}} = \sum_i \phi(x_i, y_i)
代价函数形式(Soft Penalty):
\phi(x, y) =
\begin{cases}
(d(x, y) - d_0)^2, & \text{if } d(x, y) < d_0 \\
0, & \text{otherwise}
\end{cases}
3️⃣ 为什么要使用双线性插值?
在查询控制点 P(x, y) 的距离时:
🚫 粗暴方式:最近 grid 值
d(x, y) \approx d(\text{round}(x), \text{round}(y))
🚨 问题
| 问题 | 描述 |
|---|---|
| ❌ 不可导 | 控制点移动可能导致所取 grid 突然跳变,梯度\nabla d 不存在 |
| ❌ 不连续 | 小幅移动导致代价跳变,优化器无法正确感知变化趋势 |
✅ 使用双线性插值
通过插值得到平滑函数 d(x, y):
d(x, y) = (1 - dx)(1 - dy) Q_{11} + dx(1 - dy) Q_{21} + (1 - dx)dy Q_{12} + dx dy Q_{22}
其中:
- dx = x - j,dy = y - i
- (i, j) 是控制点落入的栅格 cell 左下角
- Q_{11} = d(i, j),Q_{21} = d(i, j+1),Q_{12} = d(i+1, j),Q_{22} = d(i+1, j+1)
✅ 优势总结:
| 优势 | 描述 |
|---|---|
| ✅ 连续可导 | 便于梯度优化方法(如 L-BFGS、SLSQP、Ceres) |
| ✅ 提高精度 | 将离散地图近似为连续距离场,更精细地刻画“靠近障碍”的趋势 |
| ✅ 平滑优化行为 | 控制点微调引起的梯度响应更平稳,避免轨迹震荡 |
4️⃣ 距离与梯度计算公式
🎯 插值公式回顾
\boxed{
d(x, y) = (1 - dx)(1 - dy) Q_{11} + dx(1 - dy) Q_{21} + (1 - dx)dy Q_{12} + dx dy Q_{22}
}
✏️ 梯度推导(偏导数)
对 x 的偏导:
\frac{\partial d}{\partial x} = (1 - dy)(Q_{21} - Q_{11}) + dy(Q_{22} - Q_{12})
对 y 的偏导:
\frac{\partial d}{\partial y} = (1 - dx)(Q_{12} - Q_{11}) + dx(Q_{22} - Q_{21})
最终梯度向量为:
\boxed{
\nabla d(x, y) =
\begin{bmatrix}
\frac{\partial d}{\partial x} \\
\frac{\partial d}{\partial y}
\end{bmatrix}
}
需要特别注意的是,目前我们得到的这个梯度向量 \nabla d(x, y),仅仅是距离函数 d(x, y) 本身的梯度,而不是整个代价函数 \phi(x, y) 的梯度。
我们真正的代价项定义为:
\text{cost} = \left(d(x, y) - d_0\right)^2
要得到该代价项对控制点的梯度,需要对 cost 关于 x 和 y 进行求导,即应用链式法则:
\nabla \text{cost} = \frac{d}{dx}\left[(d(x, y) - d_0)^2\right]
= 2 \left(d(x, y) - d_0\right) \nabla d(x, y)
🔁 解释:
- \nabla d(x, y) 是从 ESDF 地图双线性插值得到的梯度,代表 当前位置向最近障碍物方向的单位向量
- d(x, y) - d_0 是当前距离与“安全距离”之间的误差
- 所以整体梯度 \nabla \text{cost} 表示“距离偏小的方向 + 靠近障碍的方向”
5️⃣ Python 可视化
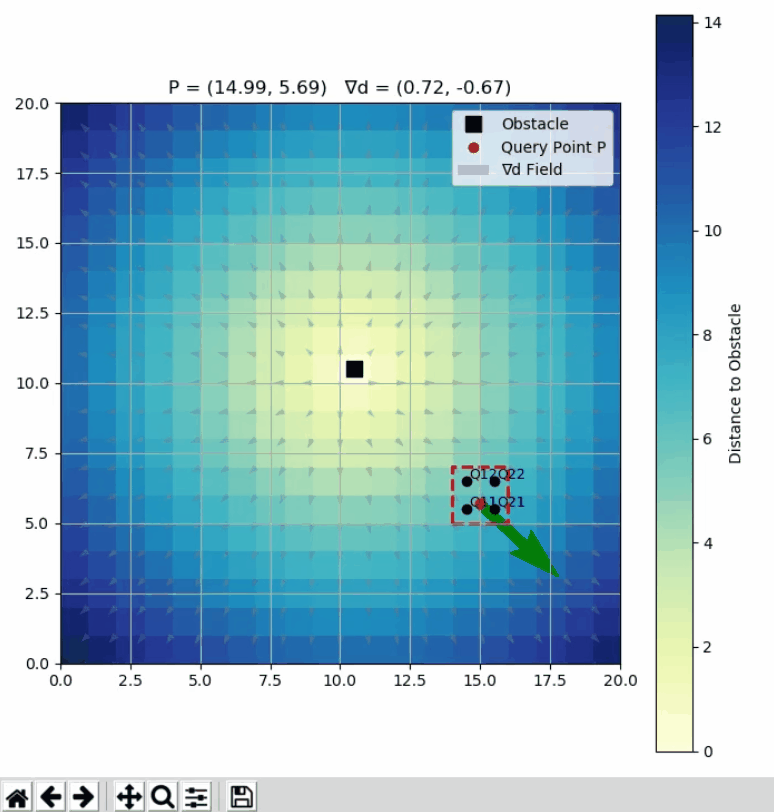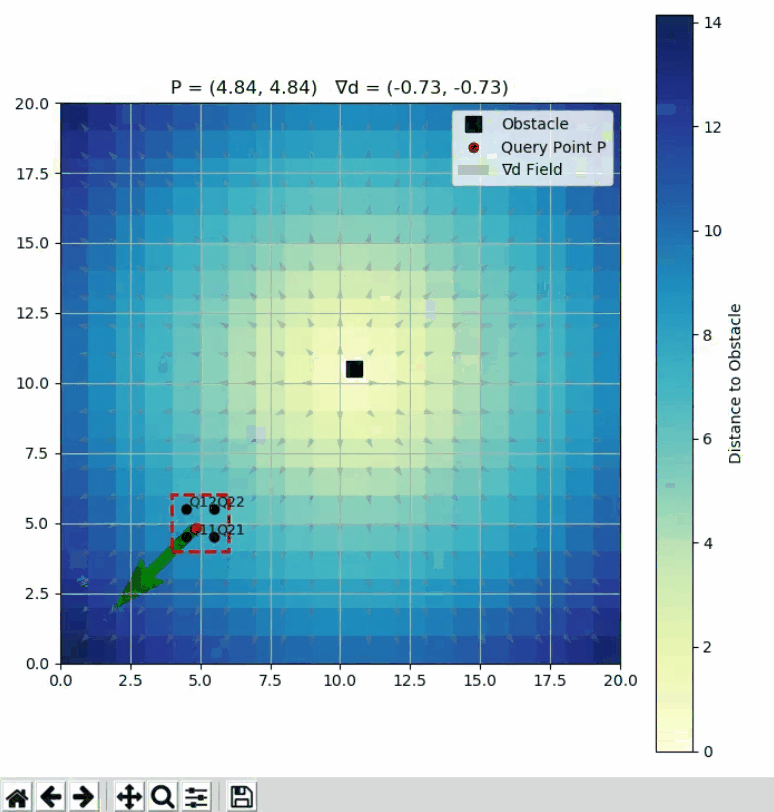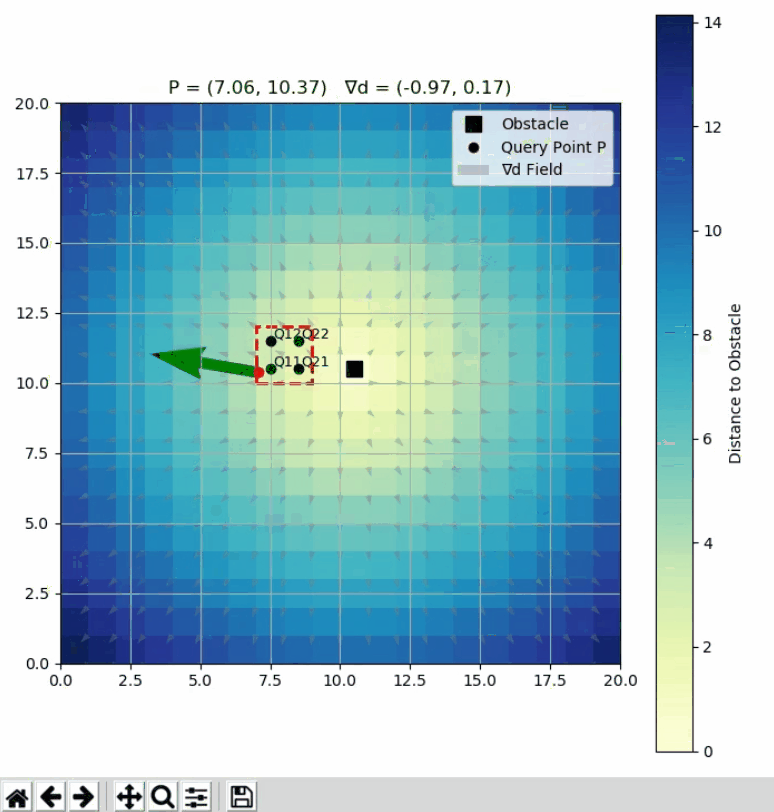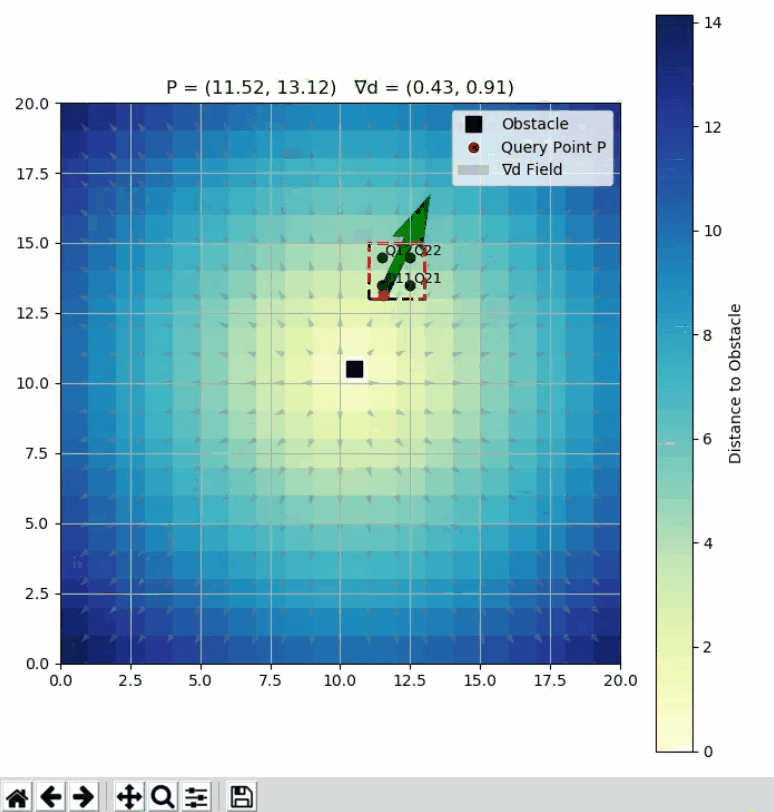
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animation
# 地图大小
H, W = 20, 20
obstacle = (10, 10)
# 生成 ESDF Distance Map
distance_map = np.zeros((H, W))
for i in range(H):
for j in range(W):
distance_map[i, j] = np.hypot(i - obstacle[0], j - obstacle[1])
# 计算整图梯度
dy_full, dx_full = np.gradient(distance_map)
# 网格坐标
X, Y = np.meshgrid(np.arange(W), np.arange(H))
# 随机查询点
np.random.seed(42)
query_points = np.random.uniform(low=2.5, high=17.5, size=(10, 2))
# 初始化图形
fig, ax = plt.subplots(figsize=(7, 7))
im = ax.imshow(distance_map, origin='lower', cmap='YlGnBu', extent=[0, W, 0, H])
cbar = plt.colorbar(im, ax=ax)
cbar.set_label("Distance to Obstacle")
ax.plot(obstacle[1] + 0.5, obstacle[0] + 0.5, 'ks', markersize=10, label='Obstacle')
ax.quiver(X, Y, dx_full, dy_full, color='gray', alpha=0.4, scale=50, width=0.005, label='∇d Field')
# 动态元素
point_plot, = ax.plot([], [], 'ro', label='Query Point P')
cell_rect = plt.Rectangle((0, 0), 2, 2, edgecolor='red', facecolor='none', linestyle='--', linewidth=2)
ax.add_patch(cell_rect)
# 用于动态添加箭头(全局变量)
grad_arrow = None
# Q 点显示
q_dots = [ax.plot([], [], 'ko')[0] for _ in range(4)]
q_labels = [ax.text(0, 0, '', fontsize=9) for _ in range(4)]
def update(frame):
global grad_arrow
query_x, query_y = query_points[frame]
i = int(np.floor(query_y))
j = int(np.floor(query_x))
if i < 0 or j < 0 or i >= H - 1 or j >= W - 1:
return
# 四个 Q 点
Q11 = distance_map[i, j]
Q21 = distance_map[i, j + 1]
Q12 = distance_map[i + 1, j]
Q22 = distance_map[i + 1, j + 1]
dx_local = query_x - j
dy_local = query_y - i
# 双线性插值求梯度
grad_x = (1 - dy_local) * (Q21 - Q11) + dy_local * (Q22 - Q12)
grad_y = (1 - dx_local) * (Q12 - Q11) + dx_local * (Q22 - Q21)
# 清除旧箭头
if grad_arrow:
grad_arrow.remove()
# 绘制新梯度箭头
grad_arrow_new = ax.quiver(query_x, query_y, grad_x, grad_y,
angles='xy', scale_units='xy', scale=0.25,
color='green', width=0.02, label='∇d at P')
globals()['grad_arrow'] = grad_arrow_new # 更新全局变量
# 更新 Query 点和 cell 框
point_plot.set_data([query_x], [query_y])
cell_rect.set_xy((j, i))
# Q 点位置和标签
q_coords = [(j + 0.5, i + 0.5), (j + 1.5, i + 0.5), (j + 0.5, i + 1.5), (j + 1.5, i + 1.5)]
q_names = ['Q11', 'Q21', 'Q12', 'Q22']
for k, (dot, label) in enumerate(zip(q_dots, q_labels)):
x, y = q_coords[k]
dot.set_data([x], [y])
label.set_position((x + 0.1, y + 0.1))
label.set_text(q_names[k])
ax.set_title(f"P = ({query_x:.2f}, {query_y:.2f}) ∇d = ({grad_x:.2f}, {grad_y:.2f})")
# 初始化函数
def init():
point_plot.set_data([], [])
for dot in q_dots:
dot.set_data([], [])
for label in q_labels:
label.set_text('')
return [point_plot, *q_dots, *q_labels]
# 动画函数
ani = animation.FuncAnimation(fig, update, frames=len(query_points), init_func=init,
interval=1200, blit=False, repeat=True)
plt.legend(loc='upper right')
plt.grid(True)
ax.set_xlim(0, W)
ax.set_ylim(0, H)
ax.set_aspect('equal')
plt.tight_layout()
plt.show()
6️⃣ 小结 🔚
| 模块 | 内容 |
|---|---|
| 插值方法 | 使用双线性插值提升连续性与可导性 |
| 安全代价函数 | 对d(x, y) < d_0 区域施加二次惩罚 |
| 梯度计算方式 | 直接对插值表达式求偏导得到梯度 |
| 优化目标函数中 | 累加每个控制点的安全代价项 |
| 最终效果 | 避障轨迹平滑、稳定、可微 |