🎯 基本定义对比
| 特性 |
Bézier 曲线 |
B 样条(B-spline) |
| 构造方式 |
单一高阶或分段拼接 Bézier 曲线 |
使用基函数 + 控制点 + knot 向量 自动构建 |
| 控制点影响范围 |
全局(高阶) 或 局部(拼接) |
局部(固定个数控制一段,滑动窗口)✔️ |
| 平滑性 |
分段需手动保持 C¹ / C² 连续 |
天然保证 C¹ / C² 连续 ✔️ |
| 插值端点 |
插值起终点(经典 Bézier) |
非插值,需特殊技巧才能强制插值 |
| 参数化 |
固定 [0, 1],均匀分布 |
支持任意非均匀 knot 分布,更灵活 ✔️ |
📐 几何与控制能力
Bézier:
- 控制点越多,曲线阶数越高,变得更难控制
- 高阶 Bézier 灵活但非常敏感 ❌
- 分段 Bézier 可局部构造,但连接点的连续性需手动调优(如重复点/对称配置)
B-spline:
- 控制点多少 ≠ 曲线阶数,稳定性更强
- 每段曲线只由
degree + 1 个控制点控制,局部调整容易
- 调节某点时只会影响临近几段 ✅
- 支持非均匀 knot,灵活调整形状与速度剖面
🔄 动态调节与可视化上的优势
| 特性 |
Bézier |
B-spline |
| 拖动中间点 |
全局影响 |
局部影响 ✔️ |
| 多段曲线 |
手动拼接 |
自动生成 ✔️ |
| 动态编辑路径 |
较难调整 |
非常自然 ✔️ |
| 可视化控制性 |
有段落断裂风险 |
连续性保障 ✔️ |
🛠️ 实际轨迹规划中常见用途
| 应用场景 |
推荐方案 |
| AGV / Robot 路径规划 |
B-spline(局部调整、可控曲率) |
| GUI / 交互设计 / SVG |
Bézier 更方便 |
| CAD/CAM 工具路径 |
B-spline / NURBS(更精细) |
💡 动画对比
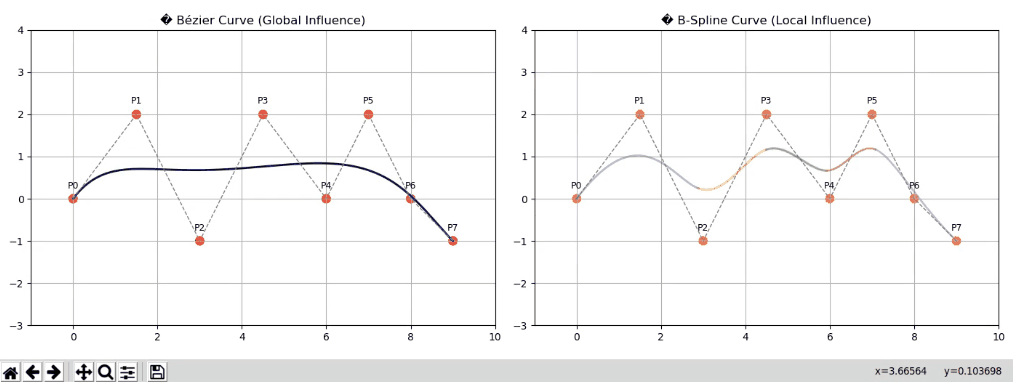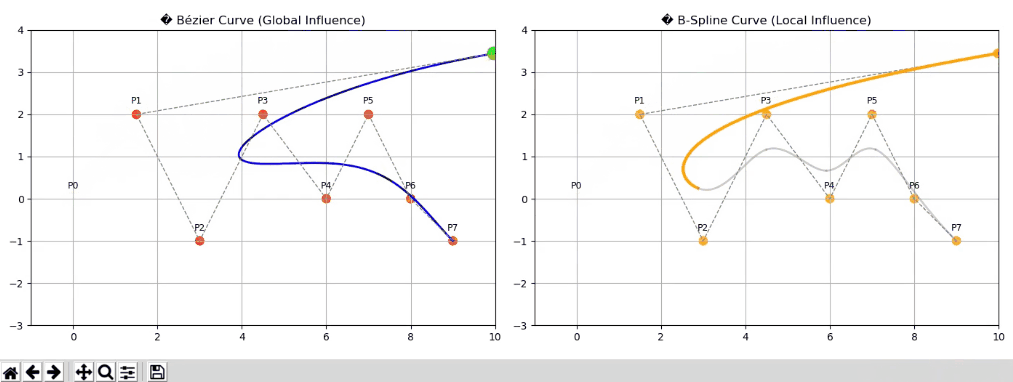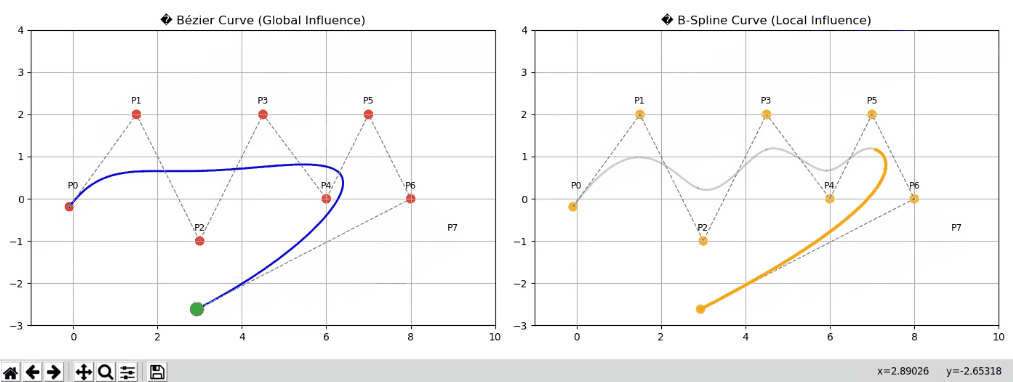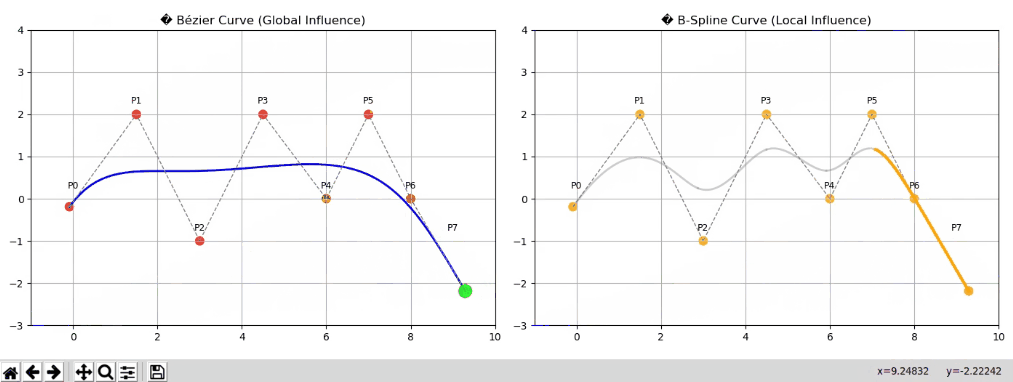
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Circle
from matplotlib.lines import Line2D
from scipy.interpolate import BSpline
# Bézier 曲线(de Casteljau)
def bezier_curve(points, n=300):
t = np.linspace(0, 1, n)
n_points = len(points)
curve = np.zeros((n, 2))
from math import comb
for i in range(n_points):
coeff = comb(n_points - 1, i) * (1 - t)**(n_points - 1 - i) * t**i
curve += np.outer(coeff, points[i])
return curve
# B样条构造
def bspline_curve(ctrl_pts, degree=3, n=200):
n_ctrl = len(ctrl_pts)
n_knots = n_ctrl + degree + 1
knots = np.concatenate((
np.zeros(degree),
np.linspace(0, 1, n_knots - 2 * degree),
np.ones(degree)
))
t = np.linspace(knots[degree], knots[-degree - 1], n)
bx = BSpline(knots, ctrl_pts[:, 0], degree)
by = BSpline(knots, ctrl_pts[:, 1], degree)
return np.vstack((bx(t), by(t))).T, knots
# 初始化控制点
ctrl_pts = np.array([
[0, 0],
[1.5, 2],
[3, -1],
[4.5, 2],
[6, 0],
[7, 2],
[8, 0],
[9, -1],
])
degree = 3
n_segs = len(ctrl_pts) - degree
# 可视化设置
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 5))
fig.canvas.manager.set_window_title(" Bézier vs B-Spline - Control Point Locality")
for ax in [ax1, ax2]:
ax.set_xlim(-1, 10)
ax.set_ylim(-3, 4)
ax.set_aspect("equal")
ax.grid(True)
ax1.set_title("Bézier Curve (Global Influence)
ax2.set_title("B-Spline Curve (Local Influence)")
# Bézier 曲线 + 控制点
bezier_line, = ax1.plot([], [], 'b-', lw=2)
bezier_ctrl_line, = ax1.plot([], [], 'gray', ls='--', lw=1)
bezier_circles = []
# B样条曲线段
bspline_segments = []
bspline_ctrl_line, = ax2.plot([], [], 'gray', ls='--', lw=1)
bspline_circles = []
# 控制点圆圈 + 拖动
class Draggable:
def __init__(self, artist, index):
self.artist = artist
self.index = index
self.press = None
self.cid_press = artist.figure.canvas.mpl_connect("button_press_event", self.on_press)
self.cid_release = artist.figure.canvas.mpl_connect("button_release_event", self.on_release)
self.cid_motion = artist.figure.canvas.mpl_connect("motion_notify_event", self.on_motion)
def on_press(self, event):
if event.inaxes != self.artist.axes: return
contains, _ = self.artist.contains(event)
if contains:
self.press = (event.xdata, event.ydata)
highlight_control_point(self.index)
highlight_bspline_segments(self.index)
def on_motion(self, event):
if self.press is None or event.inaxes != self.artist.axes: return
dx = event.xdata - self.press[0]
dy = event.ydata - self.press[1]
ctrl_pts[self.index] += np.array([dx, dy])
self.press = (event.xdata, event.ydata)
update_all()
def on_release(self, event):
self.press = None
highlight_control_point(-1)
highlight_bspline_segments(-1)
def update_all():
# 更新 Bézier
bez = bezier_curve(ctrl_pts)
bezier_line.set_data(bez[:, 0], bez[:, 1])
bezier_ctrl_line.set_data(ctrl_pts[:, 0], ctrl_pts[:, 1])
for i, c in enumerate(bezier_circles):
c.center = ctrl_pts[i]
# 更新 B-Spline
spline_pts, _ = bspline_curve(ctrl_pts, degree)
for i, seg in enumerate(bspline_segments):
t0, t1 = i / n_segs, (i + 1) / n_segs
t = np.linspace(t0, t1, 50)
bx = BSpline(knots, ctrl_pts[:, 0], degree)
by = BSpline(knots, ctrl_pts[:, 1], degree)
seg.set_data(bx(t), by(t))
bspline_ctrl_line.set_data(ctrl_pts[:, 0], ctrl_pts[:, 1])
for i, c in enumerate(bspline_circles):
c.center = ctrl_pts[i]
fig.canvas.draw_idle()
def highlight_control_point(idx):
for i, c in enumerate(bezier_circles + bspline_circles):
if i == idx:
c.set_radius(0.15)
c.set_color('lime')
c.set_zorder(10)
else:
c.set_radius(0.1)
c.set_color('r' if i < len(bezier_circles) else 'orange')
c.set_zorder(1)
def highlight_bspline_segments(ctrl_idx):
for i, seg in enumerate(bspline_segments):
if i <= ctrl_idx <= i + degree:
seg.set_color('orange')
seg.set_alpha(1.0)
seg.set_linewidth(3)
else:
seg.set_color('gray')
seg.set_alpha(0.4)
seg.set_linewidth(2)
# 添加 Bézier 控制点图形
draggers = []
for i, pt in enumerate(ctrl_pts):
c1 = Circle(pt, 0.1, color='r', alpha=0.8)
c2 = Circle(pt, 0.1, color='orange', alpha=0.8)
ax1.add_patch(c1)
ax2.add_patch(c2)
bezier_circles.append(c1)
bspline_circles.append(c2)
draggers.append(Draggable(c1, i))
draggers.append(Draggable(c2, i))
# 添加 Bézier 控制点编号
for i, pt in enumerate(ctrl_pts):
ax1.text(pt[0], pt[1]+0.25, f"P{i}", fontsize=9, ha='center', color='black')
ax2.text(pt[0], pt[1]+0.25, f"P{i}", fontsize=9, ha='center', color='black')
# 初始化 B-Spline 段
_, knots = bspline_curve(ctrl_pts, degree)
for i in range(n_segs):
line, = ax2.plot([], [], lw=2, alpha=0.5)
bspline_segments.append(line)
update_all()
plt.tight_layout()
plt.show()
⭐总结
| 对比维度 |
单段 Bézier |
分段 Bézier |
B-spline 曲线 |
| 控制点影响范围 |
🌐 全局影响,动一个点整条曲线变化 |
🔁 每段受各自控制点影响,但段与段间不连续 |
🔍 局部影响,degree+1 控制点影响一段 |
| 曲线连续性(位置 / 导数) |
✅ 位置连续,❌ 不保证导数连续 |
✅ 位置连续,❌ 不保证速度/加速度连续 |
✅ 任意阶导数连续(最多 degree-1 阶) |
| Knot 控制能力 |
❌ 无 knot,无法灵活控制段落 |
❌ 无 knot,只能分段管理 |
✅ 有 knot,精确控制每段长度与权重 |
| 支持局部修改 |
❌ 改变一个控制点会影响整条 |
✅ 改变一个段的控制点只影响该段 |
✅ 改变某段控制点,仅影响该局部段 |
| 优化控制灵活性 |
❌ 不利于局部优化(曲率、避障) |
⚠️ 可做局部优化,但段之间不连续 |
✅ 易于加入局部曲率/速度/障碍约束 |
| 高阶拟合风险(震荡) |
⚠️ 高阶 Bézier 易震荡 |
✅ 每段低阶,较稳定 |
✅ 分段管理 + 局部调节,最稳定 |
| 用于长路径拟合 |
❌ 容易震荡,不适合 |
✅ 可拼接拟合长路径 |
✅ 强项,天然适用于任意长度路径 |
| 曲率连续性与可控性 |
❌ 不保证、全局影响 |
❌ 曲率不连续,控制点处断裂 |
✅ 曲率连续且可控 |
| 拖动控制点的影响范围 |
💢 全局变化 |
✅ 只影响该段 Bézier |
✅ 只影响该段 spline,前后平滑过渡 |
| 应用示例 |
字体绘制 / 手绘轨迹 |
分段动画、插值 |
无人车、无人机轨迹规划 / 工业机器人路径生成 |
| 轨迹优化稳定性 |
❌ 全局优化困难,梯度方向易震荡 |
⚠️ 每段可独立优化,但不连续 |
✅ 收敛稳定,最常用于实际轨迹优化任务 |
| 是否工业/ROS常用 |
❌ 很少 |
⚠️ 少数应用 |
✅ 广泛使用 |
所以总的来说在机器人轨迹规划中,B样条因其局部可调、平滑连续且易于约束控制,更适合动态环境下的高效、安全路径生成