贝塞尔曲线(Bézier Curve)与B样条曲线(B-spline Curve)的推导与理解

写在前面

最近在学习Fast-Planner，觉得其中B样条曲线的优化方法非常好，并且也认识到了B样条曲线对于优化来说极其好的性质，所以准备好好学习一下

贝塞尔曲线

贝塞尔曲线的组成

贝塞尔曲线是通过给定的控制点来进行轨迹的拟合来组成的，总的来说就是由控制点+根据控制点生成的轨迹组成的

贝塞尔曲线的数学推导

对于一条多项式曲线，我们常用阶次来描述曲线的潜在复杂度复杂度(也就是表示复杂曲线的能力)，，所以这里对于贝塞尔曲线(大概先理解成一种特殊的多项式曲线？)，也可以根据阶次来描述曲线的复杂程度，贝塞尔曲线是根据控制点生成的，所以当控制点增多，就可以增加曲线的潜在复杂度。

我们定义当给定N个控制点时，生成的为一条N-1阶的贝塞尔曲线

一阶贝塞尔曲线

对于一阶贝塞尔曲线，我们拥有两个控制点P_0,P_1，时间t的取值范围为t\in[0,1]，可以写出表达式为：

p_1(t)=\begin{pmatrix}1-t\end{pmatrix}P_0+tP_1

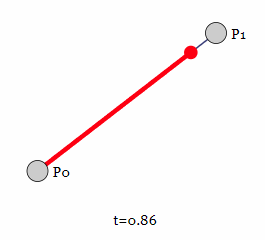
通过图像我们可以看出，一阶贝塞尔曲线是一条从P_0到P_1的关于时间t的直线p_1(t)

高阶贝塞尔曲线

二阶和三阶贝塞尔曲线

对于二阶贝塞尔曲线我们拥有P_0,P_1,P_2三个控制点，时间t的取值范围为t\in[0,1]，对三个控制点，两两生成一阶贝塞尔曲线我们可以得到：

\begin{cases}p_{1,1}\left(t\right)=\left(1-t\right)P_0+tP_1\\p_{1,2}\left(t\right)=\left(1-t\right)P_1+tP_2\end{cases}

然后此时我们在选定一个时间t的情况下，就可以得到根据p_{1,1}(t),p_{1,2}(t)生成两个点，再利用这两个点写出一个一阶贝塞尔曲线，我们就可以得出二阶贝塞尔曲线的表达式为：

p_{2}\left(t\right)=\left(1-t\right)p_{1,1}+tp_{1,2}

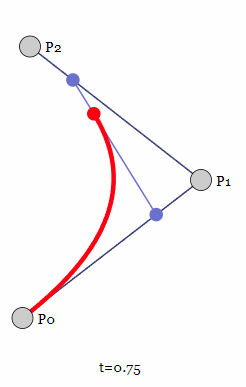
图像中蓝色的线就是根据p_{1,1}(t),p_{1,2}(t)生成的两个点写出的一阶贝塞尔曲线。

同理我们可以继续写出三阶贝塞尔曲线，拥有四个控制点P_0,P_1,P_2,P_3，时间t的取值范围为t\in[0,1]，同理，对四个控制点，两两生成一阶贝塞尔曲线，我们可以得到：

\begin{cases}p_{1,1}\big(t\big)=\big(1-t\big)P_0+tP_1\\p_{1,2}\big(t\big)=\big(1-t\big)P_1+tP_2\\p_{1,3}\big(t\big)=\big(1-t\big)P_2+tP_3\end{cases}

然后此时我们在选定一个时间t的情况下，就可以得到根据p_{1,1}(t),p_{1,2}(t),p_{1,3}(t)生成三个点，再利用这三个点两两写出一个一阶贝塞尔曲线，可以得到：

\begin{cases}p_{2,1}\left(t\right)=\left(1-t\right)p_{1,1}+tp_{1,2}\\p_{2,2}\left(t\right)=\left(1-t\right)p_{1,2}+tp_{1,3}\end{cases}

继续推导依然可以继续写出一个一阶贝塞尔曲线为：

p_{3}\left(t\right)=\left(1-t\right)p_{2,1}+tp_{2,2}

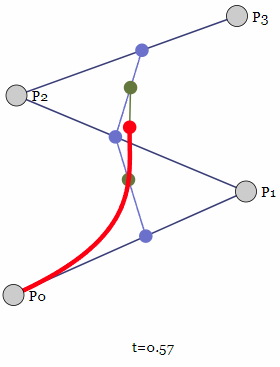
可以看到的图像中，黑色的线为控制点生成的一阶贝塞尔曲线，蓝色的线就是根据p_{1,1}(t),p_{1,2}(t),p_{1,3}(t)生成的三个点写出的两个一阶贝塞尔曲线，绿色的线就是根据p_{2,1}(t),p_{2,2}(t)生成的两个点写出的最终引导曲线的一阶贝塞尔曲线

高阶贝塞尔曲线

综上所诉，我们可以指导，高阶贝塞尔曲线也是通过一阶贝塞尔曲线逐步推导上去的，所以可以写出N阶贝塞尔的表达式：

P(t) = \sum_{i=0}^{n} P_i B_{i,n}(t) \\ B_{i,n}(t) = \binom{n}{i} t^i (1 - t)^{n - i} = \frac{n!}{i!(n - i)!} t^i (1 - t)^{n - i} \quad i \in [0, \dots, n]

其中：

i是控制点的索引
n是贝塞尔曲线的阶数
P_i是第i个控制点
B_{i,n}(t)是伯恩斯坦基多项式

所以对于这个表达式我们可以理解为每一个控制点 * 权重(伯恩斯坦基多项式)的和，伯恩斯坦基多项式可以理解为随时间变化的权重。它在贝塞尔曲线中起到了对每个控制点的权重作用，并且随着时间的变化而动态调整这些权重，使得贝塞尔曲线能够平滑地在控制点之间过渡。

贝塞尔曲线的性质

端点插值：贝塞尔曲线总是从第一个控制点开始，并在最后一个控制点结束，不会经过其他控制点。
- 在路径规划中，这条性质可以保证贝塞尔曲线能够生成一条从起点到终点的路径
凸包：贝塞尔曲线的控制点集完全包含在由这些控制点定义的凸包内。
- 这条性质是一条非常好的性质，简而言之就是贝塞尔曲线生成的曲线会被包在控制点直线连线组成的多变形中，在基于走廊的路径规划中，也就意味着，如果控制点都在安全走廊内，生成的贝塞尔曲线也会在安全走廊内。
连接处连续性：贝塞尔曲线求导依然是贝塞尔曲线：

P'(t) = \sum_{i=0}^{n-1} n (P_{i+1} - P_i) B_{i,n-1}(t)
- 根据这条性质可以写出贝塞尔曲线在起点(t=0)和终点(t=1)处的导数为：
P'(0) = n (P_1 - P_0) \\ P'(1) = n (P_n - P_{n-1})

如果我们有两条贝塞尔曲线，第一条贝塞尔曲线的控制点为P_1,P_2,P_3,P_4,第二条为P_4,P_5,P_6,P_7,此时我们只需要保证P_4-P_3与P_5-P_4相同(三点在同一条直线上)，就可以将两条曲线连接起来并且满足c^0连续(即函数连续，不存在间断点) 和 c^1连续(函数的一阶可导且导数连续)
固定时间区间：贝塞尔曲线总是定义在区间 [0,1] 上。

B样条曲线

贝塞尔曲线的缺点

在路径规划中，贝塞尔曲线的缺点主要是：

高阶曲线计算量大:贝塞尔曲线的阶数与控制点数量直接相关。对于n个控制点，贝塞尔曲线是n-1 阶的多项式。随着控制点数量的增加，贝塞尔曲线的阶数也会增加，这会导致曲线复杂度增加。高阶贝塞尔曲线容易出现振荡现象，难以控制，并且在计算上更加复杂。
不适合局部控制:调整贝塞尔曲线中的一个控制点会影响整个曲线的形状，因为每个控制点对曲线的全局都有影响。这意味着无法实现局部修改。例如，在设计复杂形状时，调整某个控制点时，可能会意外地改变其他部分的形状。
曲线分段复杂:贝塞尔曲线分段连接时，必须保证各段之间的光滑度，这需要对控制点的位置和排列进行额外的调整(例如上面提到的需要保证P_4-P_3与P_5-P_4相同(三点在同一条直线上))。特别是在复杂路径规划或图形设计中，拼接贝塞尔曲线以形成复杂形状可能会增加难度。

相对来说，B样条曲线就可以比较好的解决这些问题，B样条曲线的多项式次数可以在一定限度内独立于控制点的树木，并且允许局部控制

B样条曲线的组成

这个部分直接引用博客详解样条曲线（上）（包含贝塞尔曲线）内容

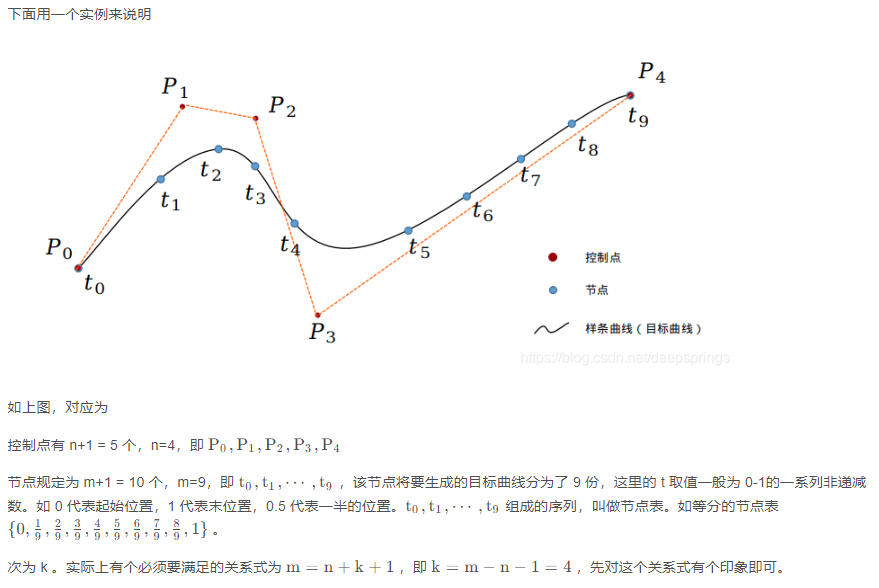
B样条曲线的推导

这个部分也直接引用博客详解样条曲线（上）（包含贝塞尔曲线）内容

直接理解一下最后这张图，这张图所代表的含义就是，如果我们想要控制t_2 - t_3这一段曲线，我们在推导时就令对应的其一阶递推值为1，其余段一阶递推值为0，那么就可以通过改变0,1,2这三个非0的基函数对应的控制点来做到只局部的改变这一段曲线

参考

动画贝塞尔曲线

详解样条曲线（上）（包含贝塞尔曲线）

路径规划算法曲线篇（二）—— B样条曲线轨迹表示详解